(上記動画のスクリプトを元に再構成したブログ版です)
今回の記事ではここまで読んできた数学的思考法・勉強法に関する本3冊のショートレビューとそれぞれの特徴の紹介、そしてこれらの本からまとめた数学的思考法に対する私見をまとめたいと思います。
では、それぞれの本の簡単な紹介から始めていきましょう。
各本の紹介
大人のための数学勉強法
まずは、「大人のための数学勉強法」。「答えをみたり覚えたりすれば基礎問題は解けるのに、初見の応用問題が解けない」。そんな悩みをどのような勉強法で解決すべきか、個別指導塾の塾長である筆者が解説した本です。
ポイントは「暗記しない」こと。論理的な流れを意識し、証明による定理の結びつきや解答に至るまでの過程を重視した勉強法を勧めています。
本質から理解する数学的手法
続いて、「本質から理解する数学的手法」。物理工学を専門とする筆者が、大学レベルの数学で必要な概念を、分野横断的に具体例を入れることで、その本質を映し出します。本質というのは、概念に関しての決まりきった数学的定義ではなく、どんなイメージか、どんな役割をしているものなのか、ということで一般的な数学の参考書とは一線を画す内容となっています。
内容は大学レベルのものが多いので、高校数学レベルからいきなり飛びつくと辛そうですが、大学に入ってから専門分野で出てくる数学につまづくような場合にはかなり有効だと思います。
数学が見つける近道
そして「数学が見つける近道」。BBCの数学史ドキュメンタリーを手掛ける一般啓蒙のプロである著者が、数学が思考における近道をどのように作ってきたのか、古今東西幅広く紹介したエッセイです。実用的な数学の利用例ということで、ここまでカバー範囲の広い本は、少なくとも私は見たことがありません。具体的な数学的知識が手に入るわけではありませんが、その思考法の実例としては大変面白く読むことができます。
無限の果てに何があるか
最後に「無限の果てに何があるか」。こちらは現代数学の基礎的な概念、とくに虚数、非ユークリッド幾何学、1+1はなぜ2なのか、といった話を中心に数学という文化の理解を深めるべく書かれた本です。ちょっと骨太な内容なので、プラスアルファとさせていただきました。「数学は人間にとって基本的な知的行為である」という考え方が根底にあり、この考え方は他の本とも共通する内容であるように思います。ここまでの本で興味が出てきたかたはぜひどうぞ。
それぞれの本の立ち位置
ではこれらの本の立ち位置ですが、まず実用と理論のバランス良く入門できるのが「大人のための数学勉強法」です。実用面では自分が学びたい内容に合っているかどうかが問題ですが、理論面はどの分野でも応用できる内容ですので、数学に苦手意識があって困っている人はぜひ読んでみてもらいたいです。高校生にもお勧めできます。
続いて「本質から学ぶ数学的手法」は大学レベルの内容となりますが、目次の項目を見ていただいて自分の理解が足りない、必要な分野があればそこをつまみ読みするのがおすすめです。
「数学が見つける近道」は読み物ですので、まだこれから数学を勉強する予定のない人、なんとなく興味があるのでちょっと知りたい人には良い一冊だと思います。
「無限の果てに何があるか」も同様に数学全般について興味がある人向けですが、専門で何かを学ぶという上ですぐさま役に立つものではないので、取り急ぎ勉強が必要な人向けではありません。
最初の3冊についてはそれぞれの紹介記事・動画もありますので、興味があればリンク先を参照いただければと思います。
数学は現実から影響を受けた思考方法であり、その思考の流れを追うと良い
では続けて、数学的思考法とその学び方について、これらの本を参考にしつつまとめた個人的意見を述べていきたいと思います。
伝えたいことを一言にまとめますと「数学は現実から影響を受けた思考方法の一種なので、思考の流れと結びつきを追うように学ぶと良い!」ということです。
まず、数学がなぜ苦手になるのかということを考えてみます。学生時代からよく聞かれる不満として「数学って何の役に立つの?」というのがあります。これって基本的には現実の概念と数学が結び付けられないことが多いから起こることではないかと思います。

例として、統計学の正規分布の式というのをみてみましょう。この正規分布というのを表す式はこんな感じです。いきなり知らない人がみると、「なにこれ、、、」ってドン引きしませんか。単独で概念だけ出されても、頭の中に結びつく要素がない場合は理解が全くできません。
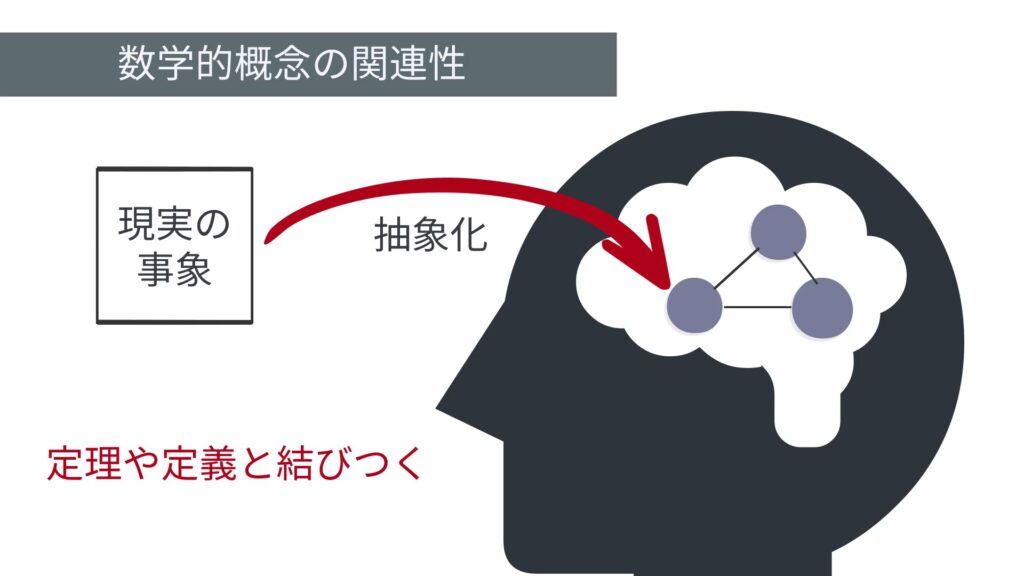
これらの数学的概念というのは基本的に現実の問題を解決する手段として、それを楽に行うために抽象化されたものであることが多くあります。また、直接的に現実に結び付かない場合でも、もともとは現実から抽象化された概念と証明を通じて結びついた定理や定義であることが多いです。またさらにそこから定理や定義が派生し、結びついていきます。
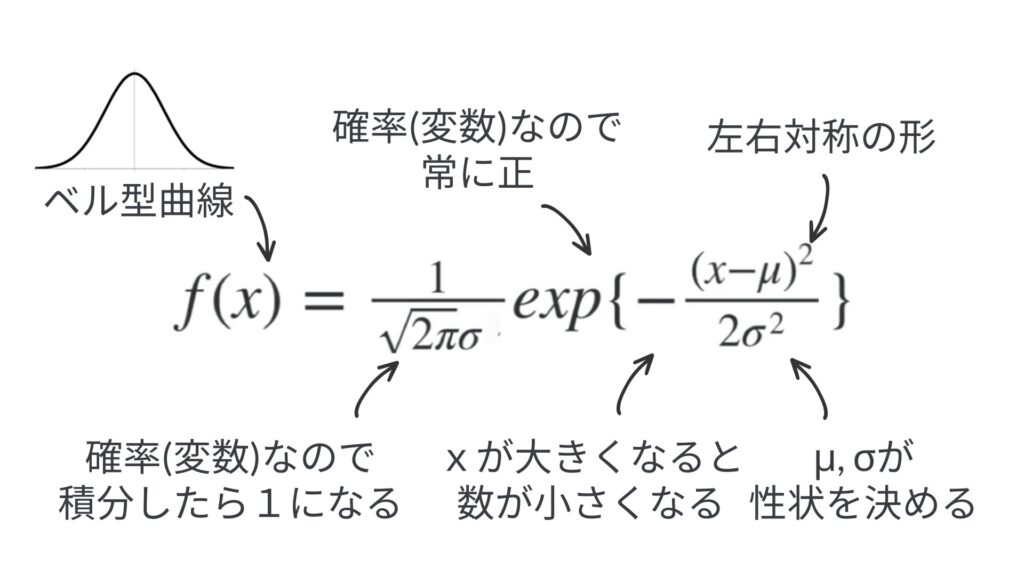
例えば、先ほどの正規分布の式の例では、少し統計学を学んでいくと色々なつながりがみえてきます。まず、この式は現実において、多数の人の身長や体重を集めた際のグラフなどでみられるベル型曲線を表す、という側面があります。また一見意味不明にみえる式も、一つ一つ役割があります。この分母は全範囲で積分したら1になる、という確率変数の定義を満たすための「正規化定数」と呼ばれる定数です。ここはネイピア数の指数となっていますが、これは確率変数が常に正であり、絶対数が大きくなると値が小さくなる、つまり大きい数は確率的に出にくくなることを表しています。さらに、二乗は左右対称であることを表しますし、μやσは平均、分散によって性状が決められることを意味します。
人によってその意味は様々ですが、このように思考の流れと結びつきがあれば、幾つも意味を見出すことができます。決してこの式だけを独立して丸覚えするものではないですね。
こうした考え方を用いると、「本質から理解する数学的手法」のように多数の現実的な事例でみることで多面的に概念を検証し、「本質」として分かり易く理解するのは良い勉強法の一つです。また「大人のための数学的勉強法」や他の本でも勧められているように証明は論理的なつながりを理解するうえで重要ですし、そこに至るまでの式の過程ひとつひとつにも思考が詰まっています。
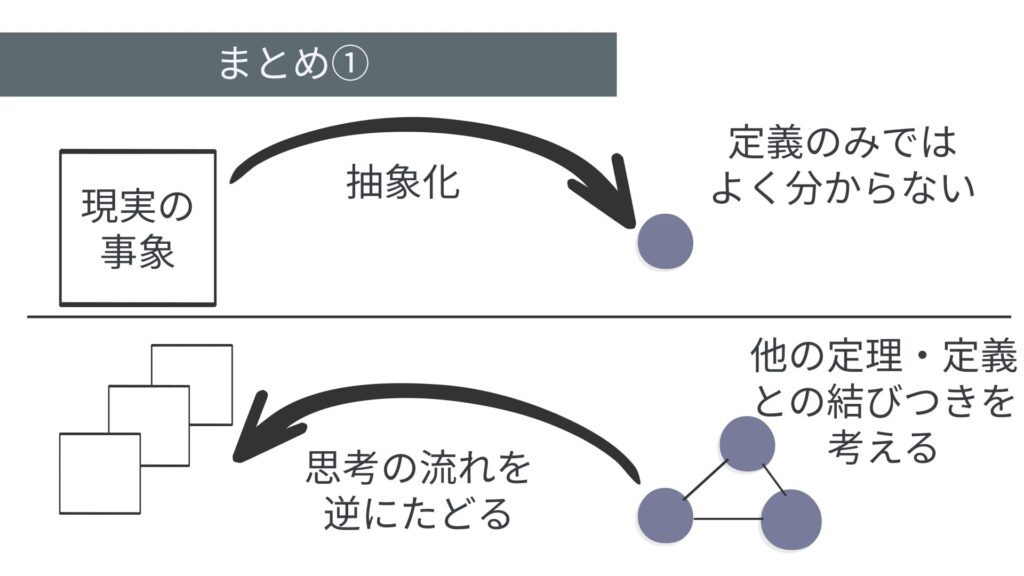
まとめ直しますと、数学は現実的概念を受けて作られる思考の一種です。抽象化されてしまっているがゆえに、その定義のみをみせられるとその意味を理解できないがほとんどです。なので、抽象化された部分を逆にたどり、現実の問題との結びつきをいくつも考えたり、他の定義や定理との結びつきを、証明を通じてたどることで、学びやすくなるはずです。
さらに、試験の応用問題や現実の複雑な問題を解く際にも「概念の結びつき」は役に立ちます。これらの問題が初見でわからないのは、複数の概念を活用する必要があり、一見それらの結びつきが分からないからです。現実の問題解決は、そもそも解けない可能性もあり、これだけで解決できるような話ではないと思いますが、少なくとも試験の応用問題はこの考え方が役立つのではないでしょうか。
私も高校時代数学が苦手でしたが、最近になって勉強する楽しさが見えてきた気がするので、これからも数学的思考と勉強法についてはまだまだ掘り下げていきたいと思います。
他にも「言語学習」「教育」「育児」「ビジネス」などなど自分の興味のある分野が多数ありますので、個々の本の紹介以外にも、今回のようにいくつか本を読んで、私見をまとめていく形式をとりたいと思います。今後もテーマをさらに掘り下げたり、広げたりしていきますので、興味のありそうな内容があればチャンネル登録して見ていただけると嬉しいです。















コメントを残す