多変数の変数変換と順序統計量が出てくる複雑そうな問題ですが、結構サクッと解けて勉強になる問題でした。
まずは多変数の変数変換から見ていきます。下三角行列が出来上がるので行列式が綺麗に求まるパターンです。与えられたYの等式を変形して
\(X_{(1)}=\frac{Y_1}{n}, X_{(2)}=\frac{Y_1}{n}+\frac{Y_2}{n-1},…,X{(n)}=\frac{Y_1}{n}+\frac{Y_2}{n-1}+…+Y_n\)
となります。微小領域に対するヤコビ行列を求めていきます。多変数変換によるヤコビアン・ヤコビ行列はこの説明が分かり易かったのでいつも見てしまいます。
行列はlatexで書くのがいつも辛いので申し訳ありませんがいつもの汚い手書きです。
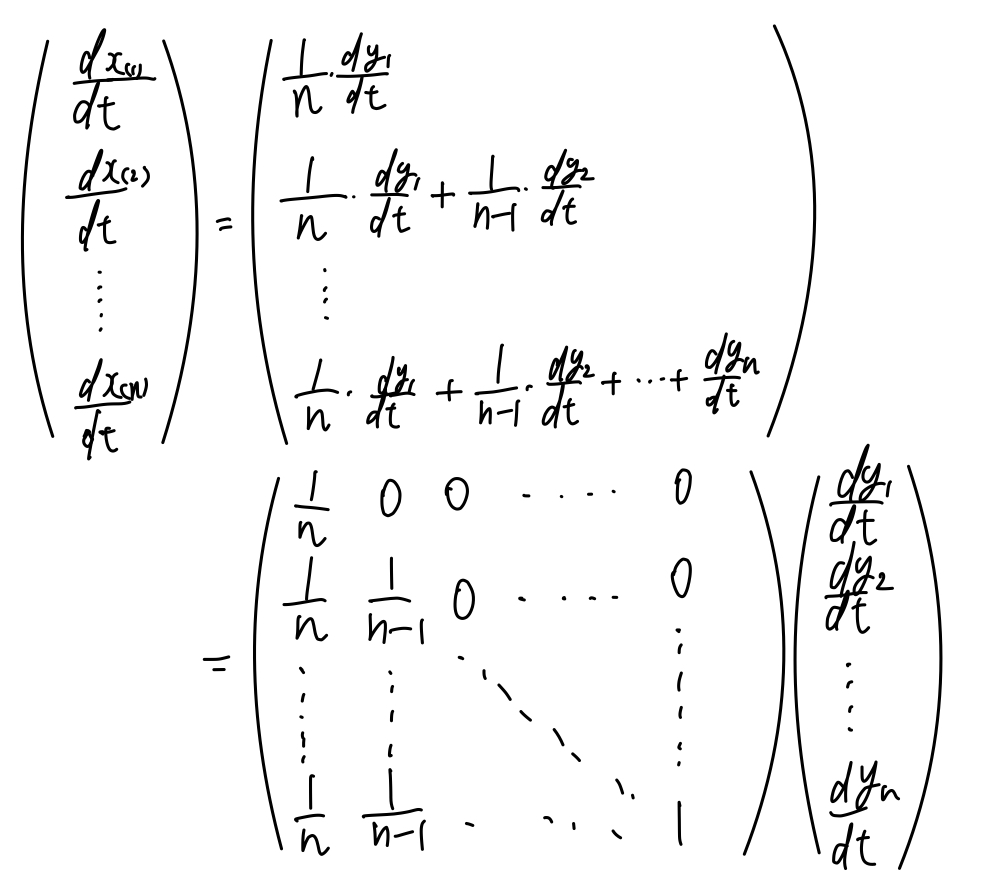
というわけで綺麗な下三角行列のヤコビ行列が出来上がります。
行列式は
\(J_{(y_1,y_2,…,y_n)→(x_{(1)},…x_{(n)})}=\frac{1}{n!}\)
となります。また順序統計量である\(X_{(1)},…,X_{(n)}\)の同時確率密度関数はn!×1~nまでの順序統計量の確率密度関数、になることを利用して
\(f_{Y_1,Y_2,…,Y_n}(y_1,y_2,…,y_n)=n!f_{X_{(1)}}(x_{(1)})…f_{(n)}(x_{(n)})\frac{1}{n!}\\=\lambda exp(-\lambda\frac{y_1}{n})\lambda exp(-\lambda\frac{y_1}{n}-\lambda\frac{y_2}{n-1})…\lambda exp(-\lambda\frac{y_1}{n}-\lambda\frac{y_2}{n-1}-…-\lambda y_n\)\\=\lambda exp(-\lambda y_1)\lambda exp(-\lambda y_2)…\lambda exp(-\lambda y_n)\)
となるため、\(Y_1~Y_n\)は独立に指数分布に従うことが示されました。
コメントを残す