実際の論文から統計を学んでみる②-ログランク検定とは-

前回から続きまして

実際の論文をみつつ統計の学習してみます。

使用している論文がこちら

“Neck weakness is a potent prognostic factor in sporadic amyotrophic lateral sclerosis patients”

(Nakamura R, Atsuta N, Watanabe H, et al Journal of Neurology, Neurosurgery & Psychiatry 2013;84:1365-1371.)

前回記事はこちら

実際の論文から統計を学んでみる① – 脳内ライブラリアン

今回はこの論文のfigure1とそこに記載されいてるp値を出す

検定方法、ログランク検定について説明してみます。

カプランマイヤー曲線の書き方については分かってる感じで

話進めますが、どこかでまたまとめるかもしれないです。

ログランク検定とは

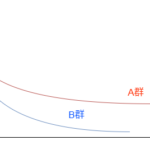
生存時間はfigure1をみてわかるように

明らかにパラメトリックな構造（正規分布っぽい構造）をしていないので

ノンパラメトリックかつ時間を考慮した検定が必要です。

ログランク検定とは

生存時間解析において、群同士を比較して

有意差があるかどうかを調べる検定です。

（否定する帰無仮説は”あるA群とあるB群が全く同じである”）

2群が基本ですが、共分散を使用して多群での比較もできます。

今回の論文では本文p1366（右中央）より

“The log-rank test was used to test the null hypothesis that all the

Kaplan-Meier curves were equal”

と書いてあるので

帰無仮説は”すべてのカプランマイヤー曲線が同じ”としていることが分かります

裏を返すと対立仮説は”すべてのカプランマイヤー曲線が同じではない”なので

多群で比較する場合、ある曲線とある曲線の2群については

有意差が出ていない可能性もあります。

※実際figure1 Fの緑と青の曲線はほぼ同じにみえます

ログランク検定は有意差を確認するための検定なので

「どれぐらいの差があるのか」は算出できません。

また、前回の記事で説明していた

比例ハザード性が保たれていないとログランク検定はできないので

注意が必要です。

具体的にログランク検定って何をやっているのか

で、これは具体的に何の数値を検定にかけているのか？

ざっくりと言うと

①2群にわけてカプランマイヤー曲線に必要なデータを出す

(被験者の死亡時点毎に死亡者数、生存者、死亡が出る前の生存者数)

②被験者の死亡時点から次の被験者の死亡時点までの

　区間について死亡者数、生存者数、死亡が出る前の生存者数を

　クロス表にする

③②について期待値を出し、実際の数値との差を求める

　分散も出す

④それぞれの時点については独立なのでの

　すべてを足し合わせた統計検定量を出す

⑤これがχ2乗検定に従うので、確率を出すことができる

、、、と書いてみると思った以上にわかりにくいので

次で詳しく書きます。

参考文献：「医薬統計のための生存時間データ解析　第2版」