※ブログ記事の商品・サービスリンクにはアフィリエイトリンクが含まれます。

医学

実際の医学論文から統計を学んでみるⅡ②-イベント数/人年データをNNTに直す方法-

前回の記事からの続きで、ELDERCARE-AF studyを題材にして考えていきます。

実際の医学論文から統計を学んでみるⅡ①-ELDERCARE-AF study/ IPCW法- – 脳内ライブラリアン

 

臨床的に解釈のしやすいのはNumber Needed to Treat(NNT)ですが、このstudyのような生存時間解析の場合は通常の計算方法ではうまく出せません。生存時間解析においてNNTをどのように出すか、を説明します。

 

 

目次：

 

人年データにおけるNNTの算出方法

通常、観察期間の決まっているRCTであれば、普通の式通りに絶対リスク減少（ARR: absolute risk reduction）をまず算出し、逆数をとれば、NNTが出ます。

 

ARR=（コントロール群のイベント数/人）- (介入群のイベント数/人)

NNT=1/ARR

 

という式ですね。ちなみにこれは介入でイベントが減るということを前提にしています。

 

ELDERCARE-AF studyで出されているのは人年あたりのイベント数なので本来はこの式とはちょっと違います。コントロール群が6.7%/人年、介入群は2.3%/人年で合計の観察人年はそれぞれ約650人年ほどでした。これを1年のあたりのイベント数が6.7, 2.3であると仮定して、無理やり当てはめてみます。

すると、

ARR=4.4%

NNT=22.727…

 

となります。

 

 

結論から先に書くと人年データの場合の正しい計算方法*1は

 

ARR={1-exp(-コントロール群のイベント数/人年)}-{1-exp(-介入群のイベント数/人年)}

NNT=1/ARR

 

です。

 

同様にstudyの結果に当てはめると

NNT=23.771

となります。

 

実は結構似通った値になるわけですが（汗

発症頻度が低い場合はあまり値は変わりません（差が出る場合は後述）。*2

 

しかし、なぜこの2つの式の違いが出てくるのか。詳細は以下で説明していきます。

 

累積発症率の伸びは徐々に緩やかになる

上述の違いは累積発症率をどういう式で推定するか、によった違いに起因します。

 

ある人が単位時間あたりイベントを発症する確率をλ（0<λ<1）、累積発症率をF(t)(tは時間)として話を進めます。

 

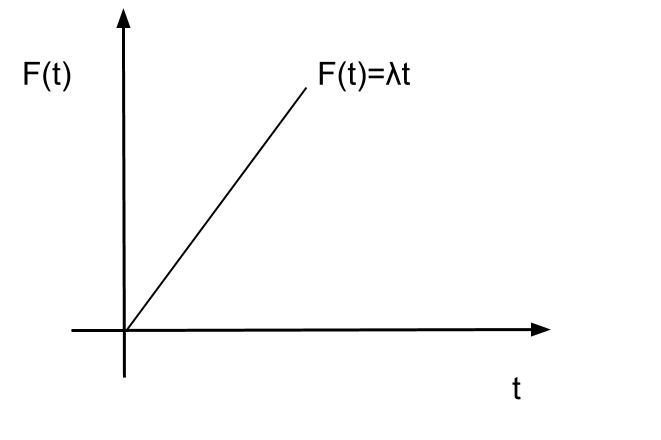
まず最初の方法の場合。コントロール群について本来約650人年の観察期間で44人にイベントがあったというもの、を単純な割り算で1人年あたり6.7人にイベントが起きたと計算しています。つまり累積発症率をλtと推測して計算しています。F(t)=λtとおけます。

 

グラフだとこんな感じです。

f:id:medibook:20200905062652j:plain

実はここが間違いで、累積発症率は時間経過する場合、徐々に伸びが緩やかになります。

 

具体的な例を考えたら分かりますが、月間20%がイベントを起こす疾患を100人に対して観察していった例で考えてみると

 

1か月後：残り80人、累積発症率20%

2か月後：残り64人、累積発症率36%

3か月後：残り51人、累積発症率49%

4か月後：残り41人、累積発症率59%

・・・

 

累積発症率の伸びが緩やかになってきているのが分かります。

 

それを考慮したモデルが2つ目の方法になるわけです。で、なぜそこにexp(自然数)が出てくるかと言うと、数式の話に入らざるを得ません（汗。苦手でない方のみどうぞ。

 

ハザード関数と指数分布

2個目の計算式を出す方法も同様に単位時間あたりイベントを発症する確率をλ（0<λ<1）、累積発症率をF(t)、それを微分したものをf(t)として説明します。

 

2個目の計算式はある瞬間における死亡率をλと考えます。

これを式にすると

①ある時間 tまではイベントが起きていないという条件のもとで

②ある時間 tから極小の時間 t+Δの間でイベントが起こる確率

となるので、①の条件付きで②が起きる確率になります。*3

 

Tをイベントが起きる時間として式をたてると

P(t\lt T\leq t+\Delta|T\gt t)\\=\frac{P(t\lt T\leq t+\Delta,T\gt t)}{P(T\gt t)}\\=\frac{F(t+\Delta)-F(t)}{1-F(t)}

となります。

 

補足ですが、縦棒｜は条件付きの意味を表します。

また前提として変形には分布関数の知識が必要です。

P(T\leq t)=F(t), P(T\gt t)=1-F(t)です。

こちらもご参考ください。

12-1. 累積分布関数とは | 統計学の時間 | 統計WEB

 

先ほどの式の両辺をΔで割って、極小と考えると微分の定義を使って

 

\frac{1}{\Delta}P(t\lt T\leq t+\Delta|T\gt t)\\=\frac{F(t+\Delta)-F(t)}{\Delta}・\frac{1}{1-F(t)}\\=\frac{f(t)}{1-F(t)}

となります。

最初の左辺こそが、瞬間の死亡率（ある極小の時間t~t+Δにイベントが起こり、かつそれまではイベントが起きていない確率）に他ならないのでλと等しくなります。

 

よって

\lambda=\frac{f(t)}{1-F(t)}

となります。

 

ここでこの関係式の両辺を0からxまでの区間で積分すると

(左辺)=\int_{0}^{x}\lambda dt=\lambda x

 

(右辺)=\int_{0}^{x}\frac{f(t)}{1-F(t)}dt=-log(1-F(x))+0

 

となるので

\lambda x=-log(1-F(x))ですから整理して

F(x)=1-exp(-\lambda x)

となります。

 

 

変数を時間のtに変えると

F(t)=1-exp(-\lambda t)

となるので、2つ目の関係式が導き出せたことが分かります。

 

今回はλを定数と考えて計算していますが、λがtに依存する関数として考えると一般的なハザード関数と呼ばれるものの定義になります。

 

二つの計算方法を並べてグラフにすると、イメージとしてはこんな感じになるので最初の方法とは違うことと、こちらの計算方法のほうが常に小さくなることが分かります。

f:id:medibook:20200906050742j:plain

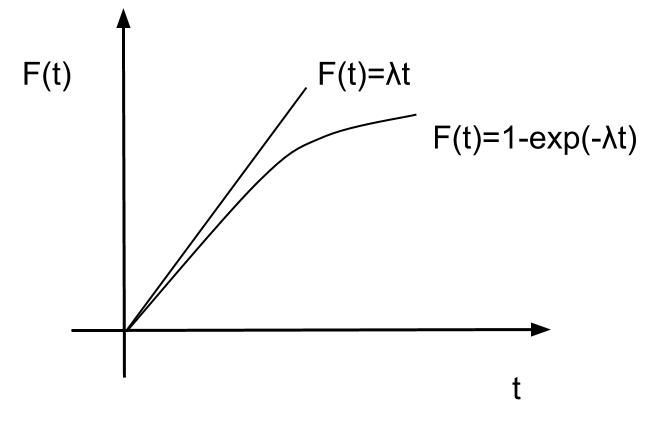
実際、二つの差をG(t)として考えると

 G(t)=\lambda t-1+exp(-\lambda t)

微分して

G'(t)=\lambda-\lambda exp(-\lambda t)\\=\lambda\{1-exp(-\lambda t)\}\\\geq0(\lambda, t\gt0)

となり、G(t)は単調増加かつ、G(0)=0なので上記のようなグラフが想定できます。

 

ただ、実際のところ、グラフの最初の方は差が小さいことが分かると思いますが、λが小さい場合（＝発症頻度が低い場合）や時間経過が短い場合は、二つの計算方法であまり誤差は出ません。なので、最初の計算でもあまり数値に差がつかなかったわけです。

 

ちなみに、F(t)を微分すると

F'(t)=f(t)=\lambda exp(-\lambda t)

となります。これは指数分布と呼ばれる確率分布になります。λを定数として考えた場合に生存時間を示す確率分布です。

 

 

話が色々と広がってしまいましたが、今回の計算方法を応用すれば、生存時間解析データから1年あたりのNNTを算出し放題なので、ぜひ臨床研究を解釈する際にお役立てください。

 

（補足）果たして計算方法で差が出るのかどうか

（2020.10.09追記） 

理論上はこの計算方法が良いですよ、と言う話なのですが、コメントでご指摘いただいたように、実際のところはあまり計算方法で差が出ることは多くないと思います。

 

差が出る例として参考文献*2に出されている例をみてみます。

それぞれ100人を１年観察した研究で、コントロール群のイベント数が80, 介入群のイベント数が40として考えます。

 

通常の方法で考えると

（コントロール群のイベント数/人）=0.8

（介入群のイベント数/人）=0.4

NNT=1/(0.8-0.4)=2.5

となります。

 

それに対して、ハザード関数の原義に忠実な計算方法で考えると(計算は省略)

NNT=4.5

となります。

 

こうなるとNNTに倍に近い誤差が出るので大きいように感じますが、こうしたことが起きるのは、例のようにかなり発症率が大きい場合ですね。

 

100人を1年観察して80%がイベントを起こすような試験ってかなり無茶苦茶です。そこまで頻度の高いかつ大事なイベントって基本的にない（重要なアウトカム＝重篤なアウトカム＝さすがにそこまで頻度は高くない）ので、まずここまでの差はないのでしょう。

 

実際の臨床試験でみられるような数％～数十％のイベント数であれば基本的にはどちらの方法でも差はあまりないと思います。手計算でできる分、通常の計算方法でも普段は十分なのでしょう。

 

(2021.06.28追記 医学論文の読み方関係の記事はこちらにまとめました) 

medibook.hatenablog.com

 

参考文献：

*1Number Needed to Treat (NNT) Calculator

情報を入れれば自動で先ほどの計算式から算出をしてくれる便利なサイトです。

*2Stang A, Poole C, Bender R. Common problems related to the use of number needed to treat. J Clin Epidemiol. 2010;63(8):820-825. doi:10.1016/j.jclinepi.2009.08.006

NNTの算出について問題点を指摘している論文です。上記サイトで引用されていました。

pubmedへのリンク

*3『現代数理統計学の基礎』

 

4件のコメント

いつも勉強させてもらっています。福岡で総合診療の研修をしている専攻医です。
NNTをフォローアップ終了時点のイベント発生率で計算するか、ハザード関数で計算するかというところについて質問させてください。
JAMA Evidence日本語版の第9章によると「これらの異なる手法は、臨床的意味が異なる結果につながることはほとんどない」とされています。
引用文献7を参照しますと(統計学の素養がなく内容は理解できていないのですが)、たしかにNNTは臨床判断を変えるほど大きく変わらないようにみえます。
正直ClinCalcを使えば手っ取り早い話かもしれないのですが、後者を使った方が良い具体例などありましたら、ご教示頂けますと幸いです。

返信

>しばにゃんさん
コメントありがとうございます。ブログをご覧いただき大変恐縮です。
実際色んな論文でその後みてみたのですが、指摘いただいている通り確かに差がないことが多いです。提示いただいた文献7も同様に実際の計算であまりNNTの誤差が生じていないことを論じているようです。記事に補足を記載しましたが、発症率が大きい場合に初めて誤差が生じてくるので、発症率がさほど高くない多くの試験ではそこまで気にしなくても良いのかもしれません。

返信

迅速なお返事や丁寧な補足まで頂いて、ありがとうございました。
実際の論文をもとにしているので、現場の研修医、専攻医のEBM教育に非常に役立つ内容だと思っています。
今後とも勉強させて下さい。

返信

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


日本語が含まれない投稿は無視されますのでご注意ください。（スパム対策）