【触って学ぶ統計学】MCMC法とは何かをわかりやすく体感する

複雑な階層パラメータを使った確率分布の話になると登場するのがMCMC法（マルコフ連鎖モンテカルロ）です。

この記事では実際のシミュレーションを触りながらMCMC法、特にMetropolis-Hastings法について学んでみます。リンク先のシミュレーションをみながら読んでみてください。

https://claude.ai/public/artifacts/e7008733-ca4c-4be0-88cb-ab6c17fcbf5a

1. ベイズ推定の基本

ベイズ推定では、知りたいパラメータの事後分布を求めることが目的です。

$$
p(\theta \mid \text{data}) = \frac{p(\text{data} \mid \theta) \cdot \pi(\theta)}{p(\text{data})}
$$

– $\theta$：求めたいパラメータ（例：治療効果の平均）
– $p(\theta|data)$：事後分布（θについて知りたい分布、これが目的！！）
– $p(\text{data} \mid \theta)$：尤度（データがθのときにどれだけ起こりやすいか）
– $\pi(\theta)$：事前分布（θに対する事前情報）
– $p(\text{data})$：正規化定数（積分の計算が必要で難しい）

知りたいのは左辺の事後分布で、パラメータがどれくらいの数値を取る可能性があるのか、を知りたいわけです。

今回のシミュレーションでは分かりやすさ重視のため分散既知の正規分布の平均θを求めることを目的にしています。

青色とオレンジの事前事後分布をみてもらうと、正規分布の形をしているのが分かると思います。

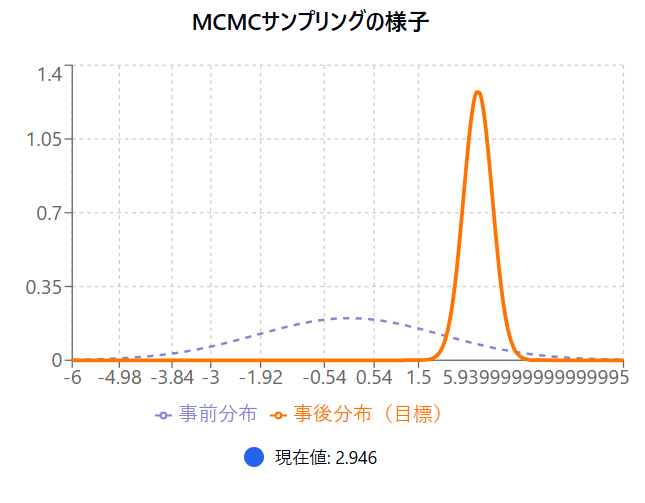
本来ここまで単純化した正規分布であればMCMC法をしなくても解析的に求められますが、分かりやすい例として用いています。

2. なぜMCMC法が必要？

事後分布を直接求めるのは、特に複雑なモデルでは困難です。
その理由は

– 正規化定数 $p(\text{data})$ の積分が計算できない
– 閉じた形で事後分布を表現できないことが多い

そこで、MCMC法を使って、本当の事後分布から得たようなサンプルを集める（サンプリングする）方法が用いられます。

3. MCMCとは？

MCMC（Markov Chain Monte Carlo）法は、

「マルコフ連鎖を使って、ある分布（事後分布）に従うサンプルを得る方法」

というものです。やり方にはいくつか種類があり、代表的な手法のひとつが Metropolis-Hastings 法です。

4. Metropolis-Hastings法のアルゴリズム

1. 初期値 $\theta^{(0)}$ を決める

2. 以下を繰り返す（m = 1, 2, …）：

シミュレーションの「MCMC開始ボタン」を押すとこのアルゴリズムが始まります。
速度バーは左に行くほど繰り返しが早くなります。

(1) 提案分布 $q(\theta^* \mid \theta^{(m-1)})$ から候補 $\theta^*$ を生成

この提案分布(proposal distribution)というのは、「現在のパラメータ $\theta^{(m-1)}$ をもとに、次に試してみる新しい候補 $\theta^*$ をどう決めるか」を定めるものです。

提案分布のよくある選び方：

– ランダムウォーク型：現在の値の近くを正規分布で選ぶ

$$
q(\theta^* \mid \theta^{(m-1)}) = \mathcal{N}(\theta^{(m-1)}, \tau^2)
$$

– 独立型：常に同じ分布から提案（\)\theta^{(m-1)}\) に依存しない）

$$
q(\theta^*) = \mathcal{N}(\mu, \Sigma)
$$

このシミュレーションではランダムウォーク型になっています。真ん中にある「サンプルの軌跡」というのをみてもらうと、パラメータθの候補が提案されて動いていく様子が分かります。

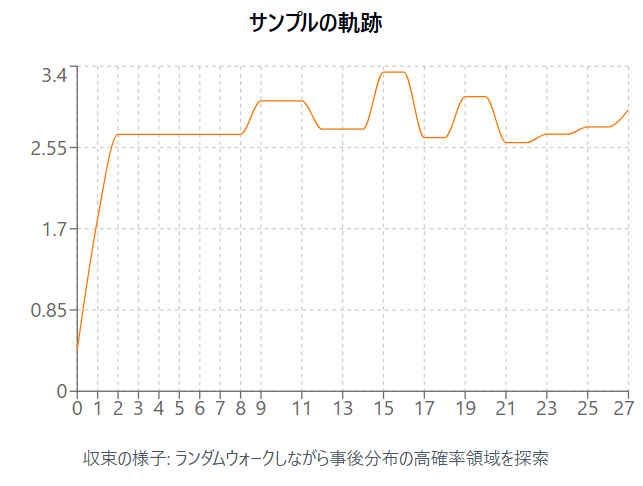
(2) 受容比（提案分布からの候補を採用するかの判断基準）を計算

候補 $\theta^*$ がどれだけ「良さそうか（＝事後分布での重みが大きいか）」を以下の比で判断します：

$$
r = \frac{p(\text{data} \mid \theta^*) \cdot \pi(\theta^*) \cdot q(\theta^{(m-1)} \mid \theta^*)} {p(\text{data} \mid \theta^{(m-1)}) \cdot \pi(\theta^{(m-1)}) \cdot q(\theta^* \mid \theta^{(m-1)})}
$$

– $p(\text{data} \mid \theta)$：尤度（データにどれくらい合うか）
– $\pi(\theta)$：事前分布（先入観）
– $q$：提案分布の確率密度

(3) 一様乱数 $u \sim \text{Uniform}(0,1)$ を生成して受容するか決定：

– $u < \min(1, r)$ の場合 → 採用：$\theta^{(m)} = \theta^*$ – それ以外の場合 → 却下：$\theta^{(m)} = \theta^{(m-1)}$

要するに少し当てはまりが悪い候補（r < 1で受容比があまりよくない）も確率的に採用されることで、局所解と呼ばれる部分的に良さそうな値にハマりこまず、分布全体を探索できるようになっています。

例えばr＝0.8とかであってもuは一様乱数ですので80%の確率で採用されるわけですね。「サンプルの軌跡」をみていくと徐々に値が定まってきますが、確率的に時々ブレが残ることが分かるはずです。

5. 正しく動作する理由（詳細バランス）

Metropolis-Hastings法は、詳細釣り合い（detailed balance）という下記の条件を満たすように設計されています

$$
\pi(\theta) \cdot P(\theta \to \theta’) = \pi(\theta’) \cdot P(\theta’ \to \theta)
$$

P(θ➔θ’)はθからθ’に変わる確率を指します。
つまりあるパラメータが別のパラメータに変わる可能性とその逆の可能性が釣り合っているわけです。
これによって、繰り返しが進むにつれて、事後分布 $\pi(\theta)$ に収束します。

シミュレーションの「MCMCの結果」というのをみると事後分布らしきものが形成されていくのがわかります。

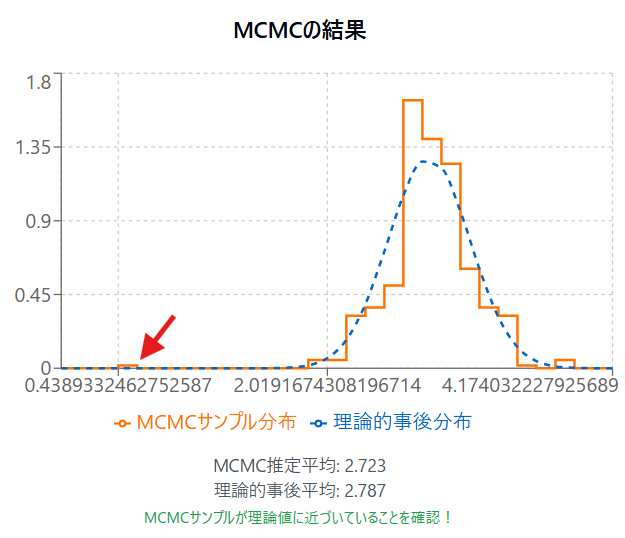
ただ実は、この画像の赤矢印のように本来の事後分布と全然違うところにサンプリングが一部されていることが分かります。これはMCMCの初期過程でパラメータの予測がまだまだ不十分なタイミングで取られたものであることが多いです。

warm upやburn inと呼ばれ、初期値に依存してしまっているため、こうした初期のサンプルは捨てることがあります。

6. 実際に行っていることのまとめ

– 尤度 $p(\text{data} \mid \theta)$ を計算する（観測データに合うかどうか）
– 事前分布 $\pi(\theta)$ をかけて事後分布に比例した形を作る
– パラメータのサンプリングを行い、この「尤度×事前分布」を用いてパラメータの候補を受け入れるかどうかを確率的に判断する
– これを繰り返すことで事後分布のパラメータの形や統計量が得られる