今日も統計検定1級の統計応用・医薬生物学分野について頻出の内容をまとめてみようと思います。
追加した内容は以前まとめた記事に載せていきます。
統計検定1級の出題範囲と過去の記事・お役立ちサイト・参考書をまとめてみた【統計検定1級対策】 – 脳内ライブラリアン
今回は、生存関数の推定値であるカプラン・マイヤー推定値(あるいはカプランマイヤー曲線)とネルソン・アーレン推定値についてです。
過去問では2016年、2019年とカプランマイヤー曲線を書かせる問題やネルソンアーレン推定値について、答えさせる問題が出題されています。
カプラン・マイヤー推定値とは
カプランマイヤー推定値は生存関数S(t)を推定するための方法の一つです。
時間tに対してある時点\(t_j\)において観察者のイベントが起きたとします。
するとその時点から次のイベント発生時点までのイベント発生率は
・\(t_j\)の直前までの観察者数を\(n_j\)(リスク集合と呼びます)
・\(t_j\)時点でイベント起こした人の数を\(d_j\)として
\(\frac{d_j}{n_j}\)と表されます。
よって、その間生存している確率は\(\frac{n_j-d_j}{n_j}\)となります。
ちなみにこの\(n_j\)には打ち切りになった人は含まれません。
というわけで、ある時点\(t_k\)までに生存している確率(=生存関数)は、それまでの時点でも当然生存していないといけません。観察者同士は互いに独立のため、確率の積を計算すると\(\hat{S}(t) = \Pi_{j=1}^{k}\frac{n_j-d_j}{n_j}\)となります。
となります。これがカプランマイヤー推定値です。さらに横軸にtをとって、縦軸にカプランマイヤー推定値を取ったものがカプランマイヤー曲線です。
さて、この具体的でない説明を最初読んだ時は自分もさっぱりわけがわからなかったのですが、具体的な例で曲線を一度描いてみることをお勧めします。
具体例
参考文献*1でも用いられている子宮内避妊用具の使用から中止までを追った生存時間解析のデータを使っていきます。
その臨床試験では開始から10、19、30週でイベントが発生(子宮内避妊用具の中止)し、13、18、23週で打ち切りが発生しています。観察者の総数は18名でした。
簡単な表にするとこのような感じです。

では順番に計算していきます。
まず10週時点で1人のイベントが発生しています。
その直前までの観察者は18名、1人のイベントが発生したので、その後の生存関数は
17/18=0.9444…となります。
よってカプランマイヤー曲線は

こんな感じになりますね。
続いて10-19週の時点では、2人が打ち切り、1人が10週までにイベント発生しているため、残り15人がリスク集合となります。そこから1人イベント発生するのでイベントが発生しない確率は14/15です。よって、19週以降の生存関数の推定値は14/15×17/18=0.8815…となります。

(グラフは理解のための参考程度で、やや適当です。縦線は打ち切りを表します。)
同様にして30週時点では1人が打ち切りで、13人がリスク集合となり、それまでの生存関数と掛け合わせて0.8137…が推定値となります。

以上がカプランマイヤー推定値とカプランマイヤー曲線でした。
ネルソン・アーレン推定値とは
カプランマイヤー法と同様に生存関数を推定する方法としてネルソン・アーレン推定値があります。
これは生存関数を以下の式で推測します。
\(\hat{S}(t) = \Pi_{j=1}^{k}\exp\left(-\frac{d_j}{n_j}\right)\)
なぜこのような式になるかですが、累積ハザード関数との関連で見てみると何となく理解しやすいようです。
生存関数と累積ハザード関数の関係性は過去の記事を参照ください。
\(H(t)=-\log S(t)\) なので
\(\hat{H}(t) = \sum_{j=1}^{k} \frac{d_j}{n_j}\)
となります。
(累積ハザード関数)=(イベント発生者数/リスク集合)の和となるので、理解しやすいように思います。
同じことをカプランマイヤー推定値に当てはめると
\(\hat{H}(t) = \sum_{j=1}^{k} \left(-\log\frac{n_j-d_j}{n_j}\right)\)
となるので、何だか理解しにくい式になってしまいます。
ただ、臨床研究の論文を読む方はご存知の通り、カプランマイヤー法の方が扱いやすいため基本的にはそちらが使われていることが多いです。
統計検定ではネルソン・アーレン推定値も問題が出ているので知っておいた方が良さそうですが、、、。
カプラン・マイヤー推定値とネルソン・アーレン推定値の関係
実はカプラン・マイヤー推定値はネルソン・アーレン推定値の近似であることが、テイラー展開を使うとわかります。
\(\frac{d_j}{n_j} = x\) とおくとマクローリン展開をすれば
\(\exp(-x) = 1 – x + \frac{1}{2!}x^2 – \frac{1}{3!}x^3…\)
となります。\(x^2\) 以降を無視すれば
\(\exp(-x) \approx 1 – x \\\approx \frac{n_j-d_j}{n_j}\)
と言えます。
上記の式から、\(x^2\) 以降の式の分だけ常にネルソンアーレン推定値の方が大きくなることがわかります。
ただ、この誤差はかなり小さいです。先程の例で見ても、たとえば最初の時点でのxは1/18となるわけですが、2乗して2で割ると、0.00154…となるのでかなり小さいことが分かります。
分母となる観察者の数がかなり少ない時は影響を受けますが、18名という臨床研究的には少ない数ですら、ほぼ問題とならないので、さらによほど少ない数でない限り気にしなくて良さそうです。
参考文献:




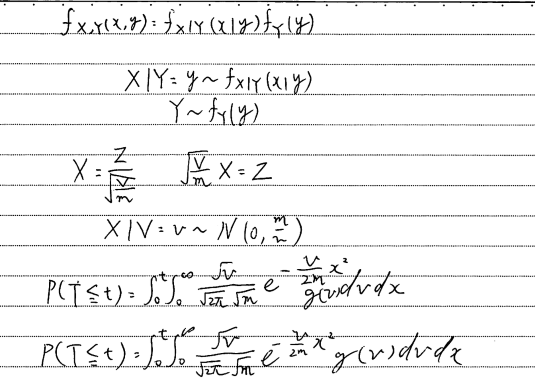










いつも参考にさせていただいております。
一点お願いなのですが、過去ページの画像が(?)表示となっているところを修正していただけると幸いです。
よろしくお願いいたします。
OTさん>
コメント有難うございます。
すみません、もともとはてなブログで運用していたため、移行時に数式を画像データとして引っ張ってきたものが
はてなブログの停止に伴い、表示できなくなっているようです。
手作業で地道な変換が必要なため中々修正ができておりませんが、特に気になるページがありましたら
優先して修正しますので、ご教示頂けますと幸いです。
よろしくお願いいたします。