統計応用医薬生物学ではときおり行列の問題が出てきます。できれば関わりたくないのですが(笑)、2022年の問3で出ている基本的な概念+αについて定義をごくごく簡単に整理しておきます。行列だけ見ていると頭がいつもこんがらがるので、今回はひたすらに成分表示をして紹介してみることにしました。
本来ベクトルは太字や斜体にしたいですし、行列もlatexで書きたいのですが、このブログだと何故かlatexだとうまく表示できません、、、。ところどころ見にくいかもしれませんが、ご容赦ください。
平均ベクトル
さて今回は確率変数Xをn次元に拡張したn次元ベクトル
\(X=(X_1, X_2,…,X_n)^T\)
について考えていきます。
まず平均ベクトルの定義は以下のようになっています。
\(E[X]=(E[X_1], E[X_2], … , E[X_n])^T\)
単純に個々の要素の期待値を取ればよいということですね。期待値は線形性がありますので平均ベクトル同士で和や差の計算も問題なくできます。
分散共分散行列
さて、続いては分散共分散行列です。定義式から展開して一度示しておくようにすると構造の理解が進むので、やってみます。まず、定義式は以下です。
\(cov(X)=E[(X-E[X])(X-E[X])^T]\)
普通の分散とそっくりな感じですね。実際どのような構造になっているか、ベクトルの成分表示をして書いてみます。
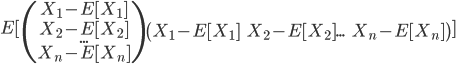
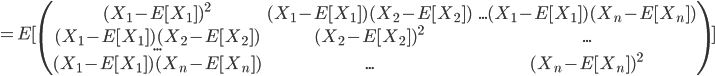
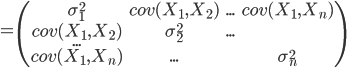
対角部分が各確率変数の分散となり、他の部分はそれぞれの確率変数どうしの共分散となることが分かります。名前の通り分散共分散を表した行列ということですね。
なお、確率変数同士がすべて互いに独立である場合は対角行列となり、共分散の部分がすべて0となります。
線形変換
さてここで、通常の変数変換と同様に行列を線形変換した場合について考えてみます。
Yをm次元ベクトルとしAはm×n行列であるとしましょう。それによってXを以下のように線形変換してみます。
\(Y=AX\)
このとき、Yの分散共分散行列はどのようになるでしょうか。
これも定義に従って式を展開すると分かります。行列なので通常の式の展開よりも注意深く進めます。(行列苦手なので、、、)
\(cov[Y]\\=E[(Y-E[Y])(Y-E[Y])^T]\\=E[(AX-E[AX])(AX-E[AX])^T]\\=E[(AX-AE[X])(AX-AE[X])^T]\\=E[A(X-E[X])\{A(X-E[X])\}^T]\\=E[A(X-E[X])(X-E[X])^TA^T]\\=AE[(X-E[X])(X-E[X])^T]A^T\\=Acov(X)A^T\)
後半部分では転置行列の変形で\((AB)^T=B^TA^T\)を使いました。
というわけでXの分散共分散行列と行列Aを使って表現することができました。
ガウス型線形回帰モデル
では続いて重回帰分析で使われるガウス型線形回帰モデルの行列表現を確認します。
成分を具体的にみて感覚をつかみたいので単回帰で行列表現を分解しながらみていきます。
まず次のような単回帰モデルを考えてみます。
\(y_i=\beta_1 X_i+\mu+\epsilon_i\)
ある結果変数yが、説明変数xと偏回帰係数β1で単回帰されており、μは固定された効果で、εは誤差変動であり、\(\epsilon_i\sim N(0, \sigma^2)\)とします。
さて、こんな感じの標本がi=0,1,2,…, nまでいるとして、説明変数xが本当に意味があるものなのかどうかを調べてみたいとしましょう。
帰無仮説を\(H_0:\beta_1=0, H_1:\beta_1\neq=0\)と設定します。
まずは全標本についてベクトルを使ってまとめてみます。
\(y=(y_1, … , y_n)^T, \beta=(\mu, \beta_1)^T, \epsilon=(\epsilon_1, … , \epsilon_n)^T\)
Xは計画行列と呼ばれ以下のようにおきます。
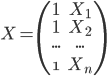
とおきます。すると
\(y=X\beta+\epsilon\)
とまとめられます。このとき\(I_n\)をn次の単位行列として\(y\sim N(X\beta_1,\sigma^2I_n)\)と多変量正規分布になっていることが分かります。
ではここから尤度関数と最尤推定量についてまず見てみましょう。尤度関数は行列を用いると次のように表されます。
\(L(\mu, \sigma^2)=\frac{1}{(2\pi\sigma^2)^{\frac{n}{2}}}exp\{-\frac{1}{2\sigma^2}(y-X\beta)^T(y-X\beta)\}\)
天下り的ですが、本当にこれが尤度関数になっているのかどうか成分表示して確認してみましょう。行列の部分に関して
\((y-X\beta)^T(y-X\beta)\)
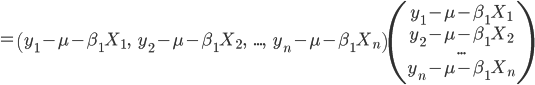
\(=(y_1-\mu-\beta_1X_1)^2+(y_2-\mu-\beta_1X_2)^2+…+(y_n-\mu-\beta_1X_n)^2\)
となりますので、元の式に入れてみると
\(\frac{1}{(2\pi\sigma^2)^{\frac{n}{2}}}exp[-\frac{1}{2\sigma^2}\{(y_1-\mu-\beta_1X_1)^2+(y_2-\mu-\beta_1X_2)^2+…+(y_n-\mu-\beta_1X_n)^2\}]\)
となります。ここで\(y_i-\mu-\beta_1X_i=\epsilon_i\sim N(0,\sigma^2)\)であることを思い出せば、この式はきちんと互いに独立な正規分布の積となっており、尤度関数となっていることが確認できます。
最尤推定量はベクトルの微分を使って算出します。以前記事にまとめました。
ここからβ1の推定量は
\(\hat\beta_1=(X^TX)^{-1}X^Ty\)
となります。
さて続いてはこの推定量の期待値と分散共分散行列をみてみます。
先ほどの線形変換の発想を使えば期待値と分散共分散行列は楽に求まります。
先ほどの例における\(A=(X^TX)^{-1}X^T\)と考えればよく
\(E[\hat\beta_1]\\=E[Ay]\\=AE[X\beta_1+\epsilon]\\=AXE[\beta_1]+0\\=(X^TX)^{-1}X^TX\beta_1\\=\beta_1\)
となり、求めたβは不偏推定量であることが分かります。
分散共分散行列は\(cov(y)=\sigma^2I_n\)であることから同様にAを用いて
\(cov(\hat\beta_1)\\=Acov(y)A^T\\=(X^TX)^{-1}X^T\sigma^2I_n\{(X^TX)^{-1}X^T\}^T\\=\sigma^2(X^TX)^{-1}X^TX(X^TX)^{-1}\\=\sigma(X^TX)^{-1}\)
となります。
さてこの分散共分散行列は今回の例の場合2×2の正方行列となっています。このうち対角成分を\(a_{11}\sigma^2, a_{22}\sigma^2\)とすると、分散共分散行列の定義から分かるようにそれぞれμおよびβ1の推定量の分散を表していることがわかります。
よって偏回帰係数β1の検定を行うには誤差ベクトルの\(\sigma^2\)を推定できれば後は良さそうです。
導出の過程はちょっと面倒なので端折りますが、σの推定量は残差平方和RSSを以下の式として次のように導出されます。
\(RSS=\sum\epsilon_i^2=\sum(y_i-\beta_1X_i-\beta)^2\\\\\hat\sigma^2=\frac{RSS}{n-k-1}\)
kは説明変数のパラメータ数なので今回は1ですね。
こうして最終的に偏回帰係数β1の推定量は以下のt分布に従います。
\(\frac{\hat{\beta_1}}{\sqrt{a_{22}\hat{\sigma^2}}}\sim t_{n-k-1}\)
これを利用すれば検定や信頼区間の算出を行うことができるというわけです。
こんな感じで展開しながら定義に従ってみていけば多少は怖くなくなるのではないかと思っております。この記事との関連問題として2022年統計応用医薬生物学問3がありますので参考にどうぞ。(記事出来次第、リンクを載せます。)














コメントを残す