前回記事に引き続いて、メタアナリシスの解釈について読む側の視点でまた少し掘り下げてみたいと思います。
前回記事はこちら
今回は欠測データの話です。欠測データがメタアナリシスに及ぼす影響について、BMJから今年面白い論文が出ていました。
m3とかcarenetのような医療系サイトでも紹介されていたので、ちらほら見た方もいるかもしれません。
欠損データはシステマティックレビューへの影響大/BMJ|医師向け医療ニュースはケアネット
メタ解析での患者の欠測データ、効果推定値に実質的な影響|BMJ|医療情報サイト m3.com
あと臨床疫学で有名な折笠先生のコメント・解説もあります。会員登録必要ですが。
イベント不明を伴うメタアナリシスではIMORによる感度分析をすべきだろう(解説:折笠 秀樹 氏)-1282|医師向け医療ニュースはケアネット
ただ、この記事だけ見ると「そもそもIMORってなんやねん、、、」と具体的な内容まで分からないので、欠測データの扱いの基本的な話も触れつつ、今回掘り下げてみることとします。
目次:
欠測データの種類
ランダム化比較試験(RCT)を行うとどうしてもアウトカムが得られない例が存在します。例えば途中で試験の同意を撤回する、転居してしまう、アウトカムと関連のない要因で死亡する、、、など。
こうして得られなかったデータのことを総称して欠測データ(missing data)と呼びます。
できるだけ減らすに越したことはないのですが、0にするのは難しいのが現実です。今回紹介した論文のintroductionで書かれていますが、638例のRCTをみたところ、欠測データのある被験者は被験者全体の9.7%(中央値、四分位範囲4.1-19.9%)だったようです。*1
これらの欠測データはその欠測する理由によって、便宜上以下の3つに分類されます。*2
①完全にランダムな欠測(missing completely at random; MCAR)
②ランダムな欠測(missing at random; MAR)
③ランダムでない欠測(not missing at rarndom; NMAR)
①、②の違いがちょっと分かりにくいですが、それぞれ具体的にみてみます。
①完全にランダムな欠測(missing completely at random; MCAR)
名前の通り完全に偶発的な理由でデータが欠測している場合です。例えば、「最初は1000人の被験者を用いて試験をしていたけれど、予算の不足で500人をランダムに選出して、残りはフォローをやめた」などですね。あまり現実的な例ではありませんが、、、。何らかの理由とは全く無関係に欠測データが生じた場合を指します。
②ランダムな欠測(missing at random; MAR)
観測されたデータに依存して、欠測するけれど、欠測値には依存しない場合を指します。例えば薬剤による血圧の変化を見たい研究があったとします。被験者を沢山集めて、そのあとで「体重が90kg以上の人は除外しよう」とした場合、観測値には依存しますが、欠測値には関係しません。こういった場合がMARと呼ばれます。後述しますが、①,②の補正はあまり問題なく行うことができるとされています。
③ランダムでない欠測(not missing at rarndom; NMAR)
これは②と異なり、欠測値に依存して欠測が生じる場合です。現実的にはこのパターンが一番多いように思います。例えば「薬の効果で脳卒中が減るかどうかをみる」試験があったとします。試験途中でアウトカムに設定されていない別の要因(例えば心筋梗塞)で死亡した人は欠測となります。すると、脳卒中を起こすような人は心筋梗塞も起こしやすい可能性が高く、「脳卒中のアウトカム」という欠測値に依存して、「心筋梗塞による死亡」という欠測が生じていると言えるので、NMARであると考えられます。これはデータの補正が容易ではありません。
欠測データの問題点と対処の方法
こうした欠測データがあると結果には当然ながら影響を及ぼします。上述したようにRCTでの欠測データの発生が被験者の約10%とすると、その被験者のアウトカムによっては結果が傾く可能性が十分あります。果たして欠測したアウトカムはどうであったのかが問題です。
欠測したデータを実際に知る術はないので、様々な方法で推測をしていく必要性があります。JAMA user’s Guides to Medical Literature*3ではイベント数に影響ないほど少なければ、推測方法の記載を省略することも可能かもしれないが、そうでなければ感度分析(さまざまな推測パターンで結果が変わるかを確認し、結果の頑健性を試す)をすべきであるとしています。今回紹介している研究でも、取り扱った論文のうち欠測データの扱いが記載されていない論文が半数近かったと問題視されています。
こうした欠測データの扱いは、細かい話をするとかなり種類があるうえに、自分の手に負えないくらい複雑になってくるので簡単に触れておきます。
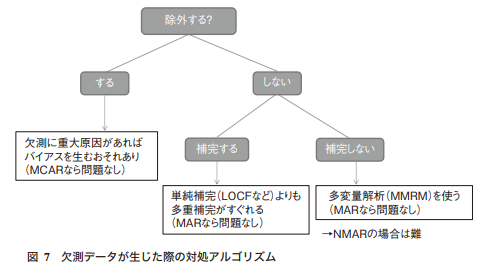
以下の図が分かりやすかったので引用します。

(*4より図を引用)
上述のうちMCARであれば、欠測データを除外しても結果は全く変わらないので問題ありません。このような除外の方法を完全ケース分析(complete-case analysis)と呼びます。
除外しない場合はデータを推測して代入する方法(上図の単純補完・多重補完、単純代入・多重代入とも呼ばれます)や代入せずにデータを推測する方法がとられます。これはMARの場合に有効です。
データを代入する方法だと、データを解析する人が欠測データの代入方法について何も知らなくても、解析ができるという利点があります。
問題なのはNMARです。MARは欠測の理由になっている観測値は分かっているので、それをもとにアレコレ推測ができますが、NMARは欠測の理由になっている肝心の欠測値が分からないので当然ながら難渋します。
ELDERCARE-Af studyで行われていたIPCW法はNMARに対する対処法の一つの例だと言えます。このstudyでは対象者が高齢であることから30%近い被験者で欠測データが生じている(!)ので、欠測データの取り扱いは必須といえます。
メタアナリシスにおける欠測データの影響
研究の内容
ようやく本題に来ました。RCTである程度起きざるを得ない欠測データの影響が、RCTを集めて作られたメタアナリシスにどれぐらい影響しているのか。それを明らかにしようとしたのが今回紹介する研究です。
具体的な方法としては2012年に出された(少し古いですね)メタアナリシス100個を集めて、そのもとになっている638個のRCTにさかのぼりつつ、欠測データの数を集計し、それを色々な解析方法で解析しなおして、結果が変わるかどうかをみています。
影響の判断をしやすいためだと思いますが、メタアナリシスはいずれも結果が2値変数(ありorなしのアウトカム)で有意差があったもの、としています。
また、この研究での解析をみていくに当たって、欠測データのある被験者はアウトカムを起こしやすいという前提があります。よく例に出されるのがAIDSに対してのanti-retroviral therapyです。*3*5フォローアップできなくなった症例を追跡調査したところ、5倍もアウトカムを起こしやすかったという結果となっています。*5 AIDSなんかは特にそうでしょうが、他の疾患でも介入群においてフォローアップできず、介入が途中でなくなった場合は大抵の場合アウトカムを起こしやすい可能性が高まると予想されます。
解析の方法
やり直した解析の方法は以下の9つとなっています。
まず、あまり説得力のない推測方法(implausible assumptions)の5つを紹介します。implausibleって訳しにくいですね。
①complete-case analysis
これは上述した通り、欠測データを全て除く方法です。たいていのRCTでは欠測データがNMARであることが多いので、この方法は間違いなくやばいです。
②best case scenario
介入群で欠測データがあった人はイベントを起こさず、コントロール群で欠測データのあった人はイベントを起こした、と想定します。嘘くさいですね。
③worst case scenario
②と逆にコントロール群で欠測データがあった人はイベントを起こさず、介入群で欠測データのあった人はイベントを起こした、と想定します。かなりの慎重派です。
④欠測データのあった人は誰もイベントを起こさなかった
⑤欠測データのある人は皆イベントを起こした
この辺は確かにimplausibleですね。
残りの4つの方法がこの研究の肝となる部分ですが、Informative Missing Odds Ratio(IMOR)という指標を用いて、解析をしています。
これは介入群において、欠測データのある被験者のアウトカムのオッズと欠測データのない被験者のアウトカムのオッズの比をとったものです。簡単に言えば、欠測データのある被験者がない人と比べてどれくらいアウトカムを起こしやすいかの指標です。これを1.5, 2, 3, 5と設定して比較をしています。最大値を5としたのは、先ほど紹介したAIDSの研究の結果を受けたものとしています。*5
具体的な例でみるとIMORの意味が分かりやすいかもしれません。
例えば介入群100名のRCTで、20名が欠測データがあり、残る80名のうち20名がイベントを起こした、とします。IMOR1.5の場合は以下のような計算をします。

同様にして、IMOR5の場合は以下のようになります。

IMORの数値によって、随分と欠測データのある被験者のオッズが変わることが分かります。
欠測データの扱いで結果はどのくらい変わったか
ここまでの内容で研究の詳細はほぼ説明したので、直接論文みて頂いたほうが分かりやすいかもしれませんが、結果は以下の図のようになっています。

IMORの値によらず大部分でオッズ比が1(つまり差がない方向)に動いているのが分かります。下に書かれた数値はもともとのオッズ比と比べて何%ほど変動したかが分かります。IMOR5だと7%ですね。
また有意差が消失したメタアナリシスの数はIMOR5では22%、IMOR1.5では6%となっています。実際のIMORがどれくらいになるかは研究内容によって違うと思うので、個人的にはAIDSのIMOR 5は高いほうだと思ってます。ただ、20%はさすがに行き過ぎにしても、5%以上ぐらいはメタアナリシスの結果も動きうるとするとなかなかの数値です。
まとめ
強固なエビデンスと称されるメタアナリシスといっても、欠測データの数によって変動しうることが実証されました。RCTについては、なおのこと欠測データの数と扱いがどうなっているかが大事です。
欠測データの扱いと何より感度分析が十分になされているかはメタアナリシスを読む上で重要であることが良く分かりました。
(2021.06.28追記 医学論文の読み方関係の記事はこちらにまとめました)
参考文献:
*1 Kahale LA, Diab B, Khamis AM, et al. Potentially missing data are considerably more frequent than definitely missing data: a methodological survey of 638 randomized controlled trials. J Clin Epidemiol 2019;106:18-31.
*2
*3jama
*4 Jpn Pharmacol Ther(薬理と治療)vol. 44 no. 7 2016
*5Geng EH, Bangsberg DR, Musinguzi N, Emenyonu N, Bwana MB, Yiannoutsos CT, Glidden DV, Deeks SG, Martin JN. Understanding reasons for and outcomes of patients lost to follow-up in antiretroviral therapy programs in Africa through a sampling-based approach. J Acquir Immune Defic Syndr. 2010 Mar;53(3):405-11. doi: 10.1097/QAI.0b013e3181b843f0. PMID: 19745753; PMCID: PMC3606953.









コメントを残す