メタアナリシスについてより詳しく学ぶ①-fixed effects model, random effects modelと異質性-

今回の記事ではメタアナリシスにおける異質性の評価について説明していきます。

メタアナリシスを読む上で、研究ごとの異質性が取り扱われているか、そしてそれが小さいのかどうかはチェックしておきたい項目です。非常に簡単な異質性についての説明は以前にも書きました。

ここまでは知っておきたいメタアナリシスの読み方⑤ -研究の異質性-

その意味をもう少し掘り下げるためには固定効果モデル、ランダム効果モデルについて知っておくことが望ましいので、今回の記事ではまずそこから説明していきます。

(2021.10.15メタアナリシスの新しいまとめ記事の一部として追記・変更しました)

前回までの記事はこちら

実臨床に役立てるメタアナリシスの読み方① システマティックレビューとメタアナリシスの違い『なぜメタアナリシスのみはダメなのか』

実臨床に役立てるメタアナリシスの読み方② -Background編〜Methods編前半

実臨床に役立てるメタアナリシスの読み方③ -Methods編中盤①

実臨床に役立てるメタアナリシスの読み方④ -Methods編中盤②

まとめたページと参考文献はこちら

実臨床に役立てるメタアナリシスの読み方まとめ

目次：

結果をどのように統合するか
fixed effects model と random effects model
モデルをどう使い分けるか-異質性の問題-
モデルによる結果の違い
異質性の評価（コクランのQ検定と）
まとめ

結果をどのように統合するか

メタアナリシス(メタ解析)というのは通常、オッズ比(OR)・リスク比(RR)・ハザード比(HR)などの結果を集めて、一つの結論を導き出すための方法です。

結果は試験によってさまざまで、数値は異なることが普通です。そこでどうやって結果を合わせていくのかをまず考えてみます。

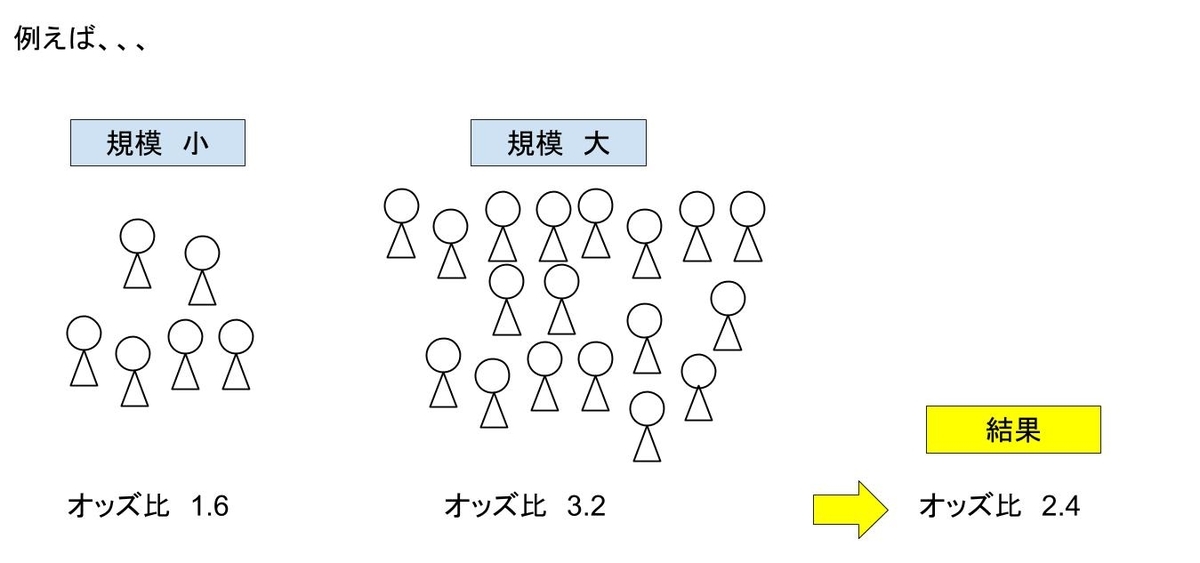
例えば、全部の結果を足して組み込んだ試験数で割る。そうすると結果は出てきますが、人数の多い試験も少ない試験も一緒くたになっているので、1000人規模の試験と100人規模の試験の結果が同じように平均化されるのは違和感があります。

（オッズ比3.2となる結果の試験のほうが明らかに被験者数が多いのに、同じレベルで統合されている）

そこで、被験者数の数が多い（＝推定誤差が少ない）試験の結果に、重みを与えて重み付き平均を出すのが、実際のメタアナリシスの方法です。

推定誤差が少ない研究であるほど、大きく扱われる（重みが大きくなる）ようにしたいので、推定誤差の逆数が重みに使われます。これはinverse variance method*1と呼ばれ、メタアナリシスの結果統合の基本の方法となります。

重みは以下の式で表現されます。*2

$\frac{1}{(各研究の標準誤差)^2}\\=\frac{各研究の例数}{各研究の測定誤差の分散}$

これを使った重み付き平均

$\frac{\{(各研究の重み)×(各研究の平均値)\}の和}{(各研究の重み)の和}$

がメタアナリシスで統合された結果となります。

数式として細かく理解できなくても、各研究の分散によって結果の大きさの扱いが変わる、というポイントが分かればとりあえずＯＫかなと思います。

fixed effects model と random effects model

こうして重みを付けて表現された各研究の結果ですが、統合にするにあたって「どこまで各研究が同じようなものであるか」が次の問題になります。

まず、各研究が施設も患者背景も、プロトコールも、outcomeの設定も非常に似たようなものである場合は、以下の式で各研究の結果をモデル化できます。

（効果の大きさ＜OR・RR・HRなど＞）=（真の効果の大きさ）+（偶然の誤差）

微妙に研究毎に結果の数値が異なるのは、（偶然による誤差）とみなして考え、他には変化する要因がないと考えます。この方法が固定効果モデル（fixed effects model）と呼ばれます。

図にするとこんなイメージです。

さて実際、医学の臨床研究においてこうしたことってあり得るでしょうか。患者背景や行われる国も違う場合がありますし、プロトコールが各施設で全く同じなんてこともまずありません。つまり各研究は異質性(heterogeneity)があるわけです。

これを評価していないと、そもそも想像される真の効果の大きさが異なるものを無理やり統一してしまうことになるわけですね。

そこで、使われるのがこの式によるモデル化です。

（効果の大きさ）＝（真の効果の大きさ）+（研究毎の偏り＝異質性の大きさ）＋（偶然の誤差）

＊研究毎の偏りは平均0, 分散 $\tau^2$ の確率変数として扱われる

それぞれの研究毎に変動する部分があり、異質性が大きいほど、これが大きくなると予測されます。こうした変動を織り込んだモデルがランダム効果モデル（random effects model）です。図にするとこんなイメージですね。

なお、ここで言われる異質性はあくまで数値的なバラツキの話であって、実質的な研究の中身までは考慮されない点に注意が必要です。つまり、仮に異質性が小さいという結果が出たとしても、研究で見ているものがまるで違う可能性もあります（以前書いたリンゴとオレンジの問題実臨床に役立てるメタアナリシスの読み方② -Background編〜Methods編前半 –）。全然違う研究の数値を並べるだけでも、数値のバラツキ次第で異質性は小さいと判断されてしまうので、そもそもの前提として同じような研究なのかどうかがまず判断されないといけません。

具体的な方法として、fixed effects modelではPetoの方法、Mantel-Haenszelの方法が知られています。random effects modelではDerSimonian-Lairdの方法が使われます。どちらのモデルかはメタアナリシスの内容にも明記はされていますが、どの方法を使っているかを見ても、どちらのモデルかが分かると思います。

ちなみにPetoの方法が初めて使われたのが1985年のこちらの論文で、メタアナリシスの説明の本*1でもこのβ blockerの話が良く出てきます。google scholarで検索すれば読めるので興味がある方はどうぞ。

Yusuf, Salim, et al. “Beta blockade during and after myocardial infarction: an overview of the randomized trials.” Progress in cardiovascular diseases 27.5 (1985): 335-371.

モデルをどう使い分けるか-異質性の問題-

で、この2つのモデルをどう使い分けるかですが、先ほどの話をみていると、そもそもfixed effects modelの前提なんて成り立たなさそうですし、全部random effects modelでいいんじゃないのと思ってしまうのですが、必ずしもそうではないようです。

どっちのモデルがいいかという解答に明確な基準と解答がないので難しいところですが、random effects modelは基本的に変動する要素を取り入れる分、結果のばらつき、つまり95%信頼区間が大きくなります。

なので、比較的研究の数が少なく、異質性が低い場合であればfixed effects modelでも良いのではないかとされています。具体的には研究の数は5未満、異質性は基準はありませんが、0%に近いことが望ましいようです。*1

実際のところモデル選択で違いが出るメタアナリシスはどれくらいあるのか、ということですが、メタアナリシス全体でみたとき20%ぐらいとされています*1。

これは509例のメタアナリシスを分析したこちらの論文*3をもとにして、語られているようで、確かに過去に出たものでは異質性が小さいものが結構多いようですね。2003年の論文であるため、今と比較するには古いかもしれません。グラフはこちらで、縦軸がメタアナリシスの数、横軸が異質性となっています。（異質性が大きいものも、それなりにあるのは気にかかります・・・）

（文献*3より引用）

モデルによる結果の違い

fixed effects modelとrandom effects modelでは結果について違いが出ます。なので、結果を解釈する際にモデル毎の特性を頭に入れておく必要があります。

ひとつにはうえで触れたように、random effects modelは各研究毎の変動する確率変数がなかに入っている分、変動幅が大きいことを想定するため、95%信頼区間が大きくなります。

もうひとつは結果の値自体も変わることがあります。random effects modelでは小さい研究にもある程度重みが置かれやすいため、そちらに引っ張られた結果となります。それに対してfixed effects modelでは被験者数が多い研究の結果に、より引っ張られやすいので、モデルによって結果の違いが生じることがあります。

なお、異質性が小さければこれらの違いは小さくなります。固定効果・ランダム効果の各式をもう一度並べて見てみましょう。

（効果の大きさ）=（真の効果の大きさ）+（偶然の誤差）

（効果の大きさ）＝（真の効果の大きさ）+（研究毎の異質性）＋（偶然の誤差）

異質性が0であれば二つの式は一致します。つまり、異質性がなければどちらのモデルも同じであり、結果や信頼区間は変わらなくなるわけです。

異質性の評価（コクランのQ検定と $I^2$ ）

では、ランダム効果モデルと固定効果モデルの違いである研究ごとの異質性をどのように評価したら良いのか。研究毎の異質性がどのように計算されるか、概略を説明してみます。

以前はメタアナリシスをする際に、それぞれの研究が本当に均質なものなのかどうか、これを検定して確認していました。その一つがコクランのQ検定(Cochran’s Q test)です。例えばオッズ比を結果とするものであれば、式は以下のようになります。結果がK-1（Kは組み入れた研究数）のカイ二乗分布に従うので検定にかけることができます。

$Q=(各研究の重み)×\{(各研究の対数オッズ比)-(統合された対数オッズ比)\}^2の和\sim\chi^2_{K-1}$

この検定は「異質性があること」を帰無仮説としているわけですが、この検定方法の問題は少数の研究を組み入れたメタアナリシスで明らかに結果の傾向が似通っていても、有意性が出なかったり（仮説検定の原則通り、有意差が出ない＝異質性がある、とは言えない）、また逆に多数の研究のメタアナリシスで異質性がない、と出たり、要するにこれだけを指標にするには無理があったわけです。*3

そこで登場したのが $I^2$ という異質性の指標です。

この数値は以下の式で計算され、0〜100％の数値となります。

$I^2=\frac{Q-(K-1)}{Q}×100$

これだと何を意味しているのかわかりづらいのですが、実はこの式は以下のように変形できます。*2

$I^2=\frac{Q-(K-1)}{Q}×100=\frac{\hat\tau^2}{\hat\sigma^2+\hat\tau^2}×100$

$\hat\tau^2$ はランダム効果モデルにおける真の値θの分散（異質性の大きさ）であり、 $\hat\sigma^2$ は研究毎の誤差の分散です。

つまり、異質性の大きさが全体の誤差の大きさ（異質性の大きさ＋研究毎の誤差の大きさ）に占める割合を示しているわけです。

最近のメタアナリシスではほとんどの場合この $I^2$ が示されていると思います。「異質性が大きいのに固定効果モデルを用いている」なんていうことがあれば、結果がモデルによって変わっている可能性もあるので注意が必要です。

まとめ

・固定効果モデルとランダム効果モデルの二つの特徴を表にまとめると以下のようになる

・異質性を考慮したモデルがランダム効果モデル

・異質性の大きさの指標として $I^2$ があり、0％であれば固定効果/ランダム効果での違いは生まれない

新しく書いたメタアナリシスのまとめ記事の一つとしてリライトしました。次はメタアナリシスの結果の解釈について書いていきます。

参考文献：

リンク

EBMを学ぶ上で必携の一冊です。難しい数式は登場せず、実臨床でエビデンスを扱う医師が知るべき内容が網羅されています。情報量が膨大なので、通読はできないと思いますが、論文を読んだり、抄読会で発表するたびに、関連するページをみるだけで十二分に役立つと思います。研修医時代から買っておけばもっと論文を見る目も早く養われただろうな、、と悔やまれる一冊です。それぐらいオススメ。

リンク

英語を読みたくない方向けに、日本語版もあります。

リンク

ガチな数学も出てくるメタアナリシスの解説書です。式の根本的な解釈でもう少し解説があると嬉しいところです。現在読書中。

*3 Higgins, Julian PT, et al. “Measuring inconsistency in meta-analyses.” Bmj 327.7414 (2003): 557-560.