明けましておめでとうございます。
さて、今年も統計の勉強記事からあげていきます。
統計検定1級において確率分布は基本事項として問題を解く際に前提知識として必要なことも多いですが、その特徴自体が問題として問われることもあります。
しかしながら、しょっちゅう統計の問題解いているわけでないと、すぐ忘れてしまうんですね。大学受験時代の記憶力はもはや保たれていないようです(汗
というわけで、統計検定1級で出てくる代表的な確率分布をすぐ思い出せる&覚えやすくするために簡易にまとめてみます。自分の備忘録的な意味合いが強いです。細かい説明はないので、ある程度基本は知ってるけど試験のためなどで確率分布を覚えたい方、ご利用ください。今回は離散型についてです。
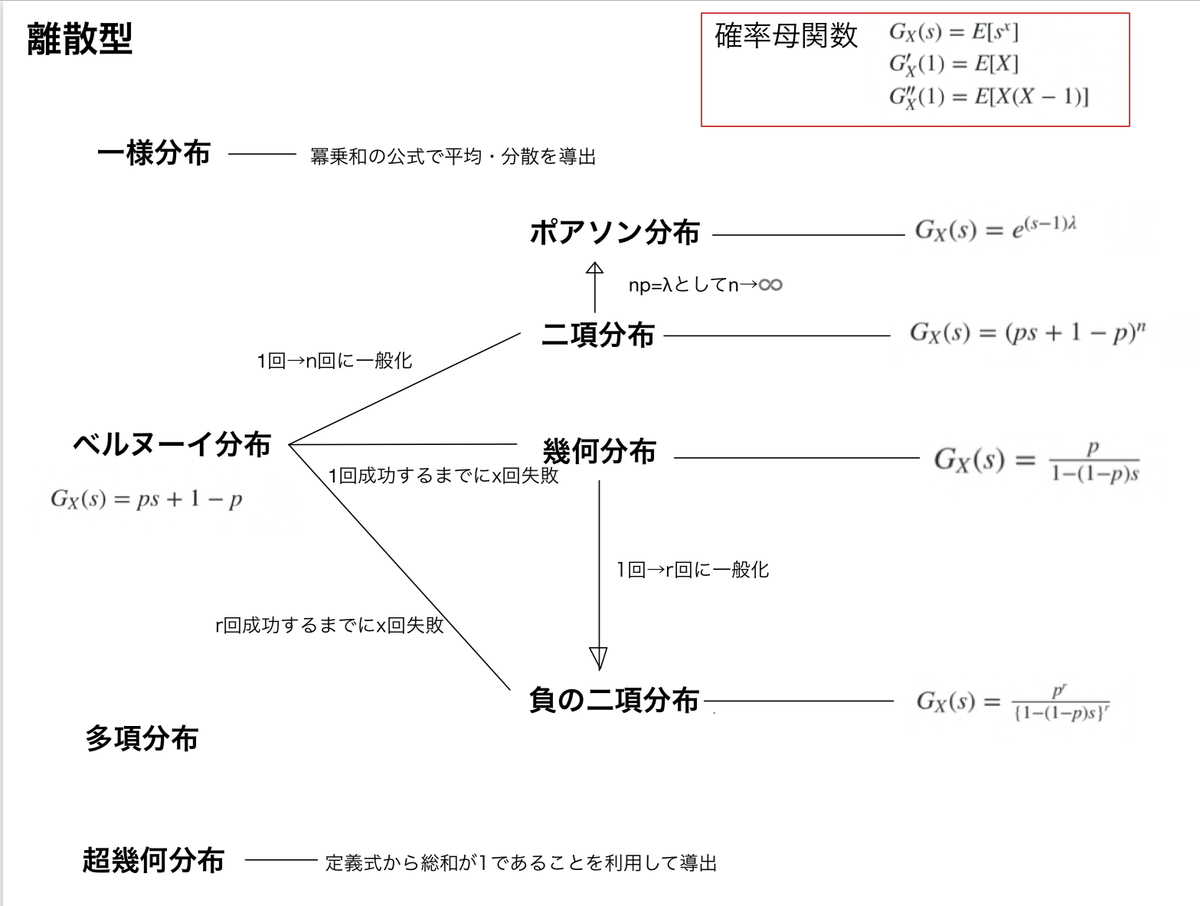
図にしてまとめる
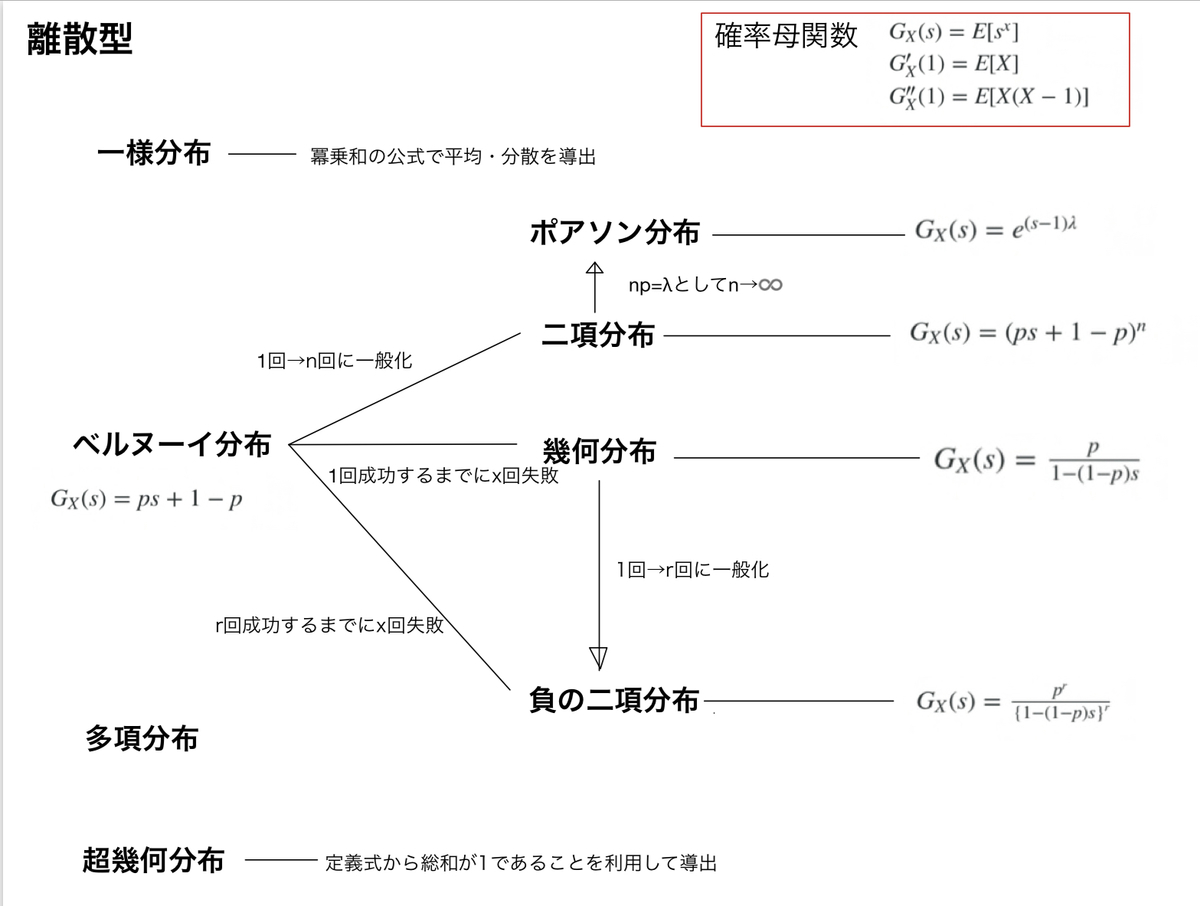
確率母関数がわかれば、期待値や分散の導出は楽なので、ひとまずそれだけ書いてます。確率母関数が容易でないものは、期待値・分散の導出方法を書いてます。多項分布についてはあまり触れてませんが、、、。
ちなみに確率母関数は簡単に言えば、微分して1を代入することで下記の式の期待値を簡単に出すことができる道具みたいなもんです。
*べき乗和の式で1、2次のモーメントは簡単に計算できる
②ベルヌーイ分布
確率母関数は \( G_X(s) = ps + 1 – p \)
③二項分布
確率母関数は \( G_X(s) = (ps + 1 – p)^n \)
*導出には2項定理を用いると良い
\[ (a + b)^n = \sum_{x=0}^n {_n C_x} a^x b^{n-x} \]
*ベルヌーイ分布と比べるといずれもよく似ている
*分布の再生性がある
④ポアソン分布
確率母関数は \( G_X(s) = e^{(s-1)\lambda} \)
*平均も分散も実は二項分布と一緒(pが限りなく小さいので1−p→1となっている)
*分布の再生性がある
⑤幾何分布
\( P(X = x | p) = p(1 – p)^x \)
確率母関数は \( G_X(s) = \frac{p}{1 – (1 – p)s} \)
*導出には初項 \( p \)、比を \( (1 – p)s \) とする等比数列の和になることを利用する
*無記憶性が特徴、連続型では指数分布に相当する
⑥負の二項分布
\[ P(X = x | p) = {x + r – 1 \choose x} p^r (1 – p)^x \]
確率母関数は \( G_X(s) = \frac{p^r}{\{1 – (1 – p)s\}^r} \)
*幾何分布の母関数をr乗したものとなっている
*ベルヌーイ分布と二項分布の変化と全く同様となっている
*連続型ではガンマ分布に相当する
⑦多項分布
\[ P(X = x | p, n, K) = \frac{n!}{x_1! \cdots x_K!} p_1^{x_1} \cdots p_K^{x_K} \]
\[ E[X_i] = np_i \quad (i = 1, 2, \dots, K) \]
\[ V(X_i) = np_i(1 – p_i) \]
*導出は*1を参考
⑧超幾何分布
\(P(X=x|N,M,n)=\frac{_MC_x・_{N-M}C_{n-x}}{_NC_n}\)
*他の分布に比べてぼっち感がありますが、フィッシャーの直接確率検定やログランク検定にも関わるので大事です
\[ E[X] = \frac{nM}{N} \]
\[ V(X) = \frac{nM}{N} \left( 1 – \frac{M}{N} \right) \frac{N-n}{N-1} \]
*導出過程がテクニカルで大変です、概略については過去に記事書きました
参考文献:














コメントを残す