ワイブル分布の期待値と分散【統計検定1級対策】

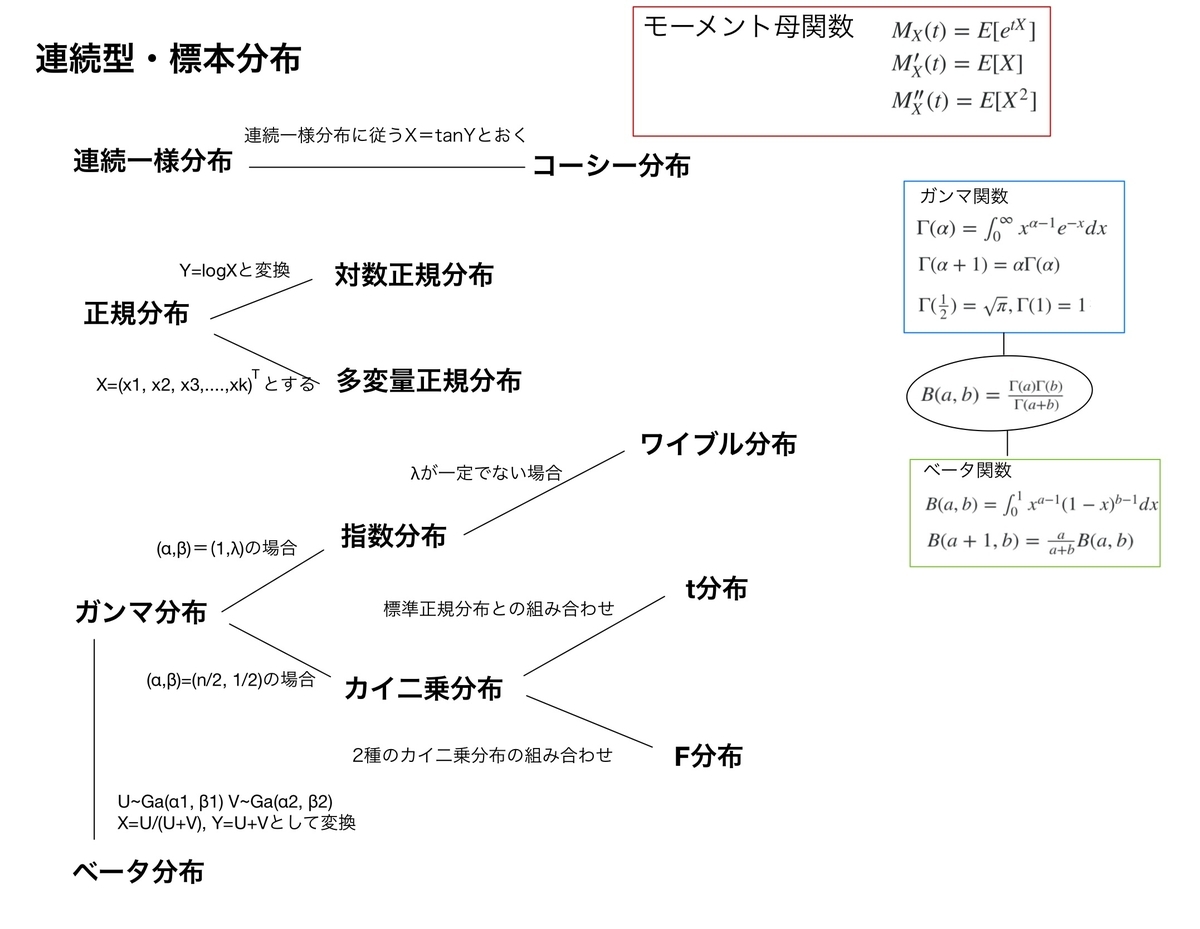
別記事で代表的な確率分布についてまとめていますが、文量が増えそうなのでワイブル分布の平均と分散の計算はここでまとめてみます。

そういえばワイブル分布については今までほとんど問題も解いたことなかったですし、馴染みがあまりありませんでした。

ワイブル分布の式は『現代数理統計学の基礎』に倣って

\[
f(x) = abx^{b-1} \exp(-ax^b)
\]

としておきます。

期待値の導出

定義通りに計算します。

\[
\int_0^\infty xabx^{b-1} \exp(-ax^b)dx
= \int_0^\infty abx^b \exp(-ax^b)dx
\]

ここで ( ax^b = t ) として置換します。すると

\[
\int_0^\infty \left(\frac{t}{a}\right)^{\frac{1}{b}} \exp(-t)dt
= a^{-\frac{1}{b}} \Gamma\left(\frac{1}{b} + 1\right)
\]

となります。

分散の導出

これも二次のモーメントからゴリゴリ計算します。

\[
\int_0^\infty x^2 abx^{b-1} \exp(-ax^b)dx
= \int_0^\infty abx^b \exp(-ax^b)dx
\]

\[
= \int_0^\infty \left(\frac{t}{a}\right)^{\frac{2}{b}} \exp(-t)dt
= a^{-\frac{2}{b}} \Gamma\left(\frac{2}{b} + 1\right)
\]

これをみるとワイブル分布のn次モーメントは
\[
a^{-\frac{n}{b}}\Gamma\left(\frac{n}{b}+1\right)
\]という単純な形で推測できることが分かります。

よって分散は

\[
V(X) = E[X^2] – (E[X])^2
\]\[
= a^{-\frac{2}{b}}\Gamma\left(\frac{2}{b}+1\right) – a^{-\frac{1}{b}}\Gamma^2\left(\frac{1}{b}+1\right)
\]\[
= a^{-\frac{2}{b}}\left{\Gamma\left(\frac{2}{b}+1\right) – \Gamma^2\left(\frac{1}{b}+1\right)\right}
\]となります。