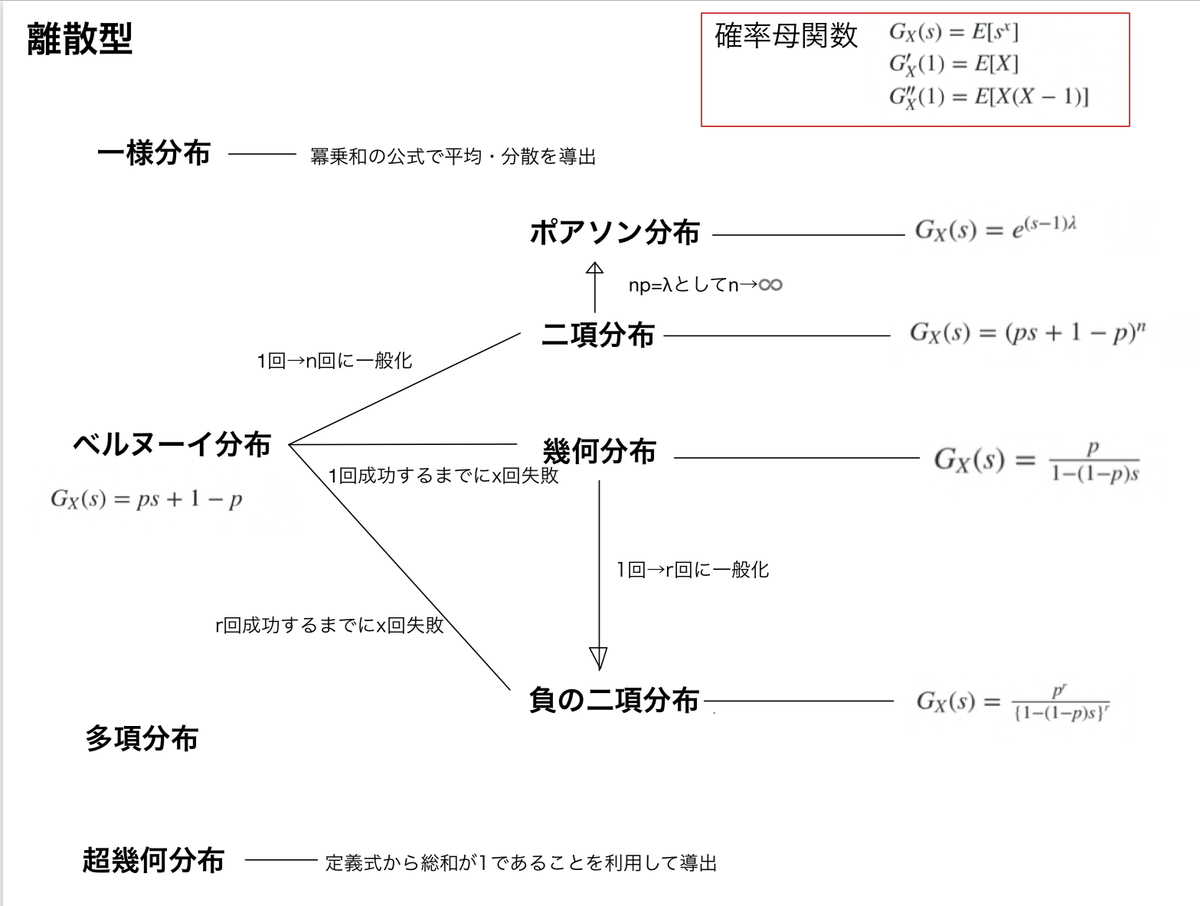
引き続いて、問7(3)です。
(2)で出てきたZがどんな分布になるかという問題。
公式の解答では当然のごとく、ガンマ分布に従う確率変数 \(X, Y\) であれば
\[
\frac{X}{X+Y} \sim B(n,m)
\]
となっています。
せっかくなので証明をやってみます。
まずは変数変換を用います。
\[
\frac{X}{X+Y} = Z, \quad X+Y = W
\]
とします。
すると
\[
X = WZ, \quad Y = W(1-Z)
\]
となります。
ヤコビアンを求めます。
\[
J = -wz – w(1-z) = -w
\]
同時確率密度関数に代入
\[
f_{w,z} = \frac{\theta^n}{\Gamma(n)} (wz)^{n-1} \exp(-\theta wz) \cdot \frac{\theta^m}{\Gamma(m)} \{w(1-z)\}^{m-1} \exp\{-\theta w(1-z)\} w
\]
\[
= \frac{\theta^{n+m}}{\Gamma(n)\Gamma(m)} w^{n+m-1} z^{n-1} (1-z)^{m-1} \exp(-\theta w)
\]
かなりベータ分布らしい形になってきました。
不要な \(w\) を消去し、\(z\) の周辺確率密度関数を求める
\[
f_z = \frac{1}{\Gamma(n)\Gamma(m)} z^{n-1} (1-z)^{m-1} \int_0^\infty (\theta w)^{n+m-1} \theta \exp(-\theta w) dw
\]
\(\theta w = t\) と置換すると後半部分はガンマ関数になるので
\[
= \frac{\Gamma(n+m)}{\Gamma(n)\Gamma(m)} z^{n-1} (1-z)^{m-1}
\]
\[
= \frac{1}{B(n,m)} z^{n-1} (1-z)^{m-1}
\]
となります。
後の有意水準はベータ分布を使って解答通り範囲を示せばおしまいです。














コメントを残す