※ブログ記事の商品・サービスリンクにはアフィリエイトリンクが含まれます。

統計2022.03.25

【統計応用・医薬生物学】ノンパラメトリック法・ウィルコクソンの符号付き順位検定【統計検定1級対策】

引き続きノンパラメトリック法の検定についてみていきます。

ウィルコクソンの符号付き順位検定とは

ウィルコクソンの符号付き順位検定は1標本の検定に使われるもので、対応するデータの差が正のときに1、負のときは0として（ここまでは符号検定と同じ）それにデータの差の大きさの順位を掛け合わせることで検定を行うものです。

符号検定と異なり、データの分布が中央値に対して対称でないといけない点が注意が必要です。

具体例で考えてみる

符号検定の記事で使ったのと同じ例を出してみます。

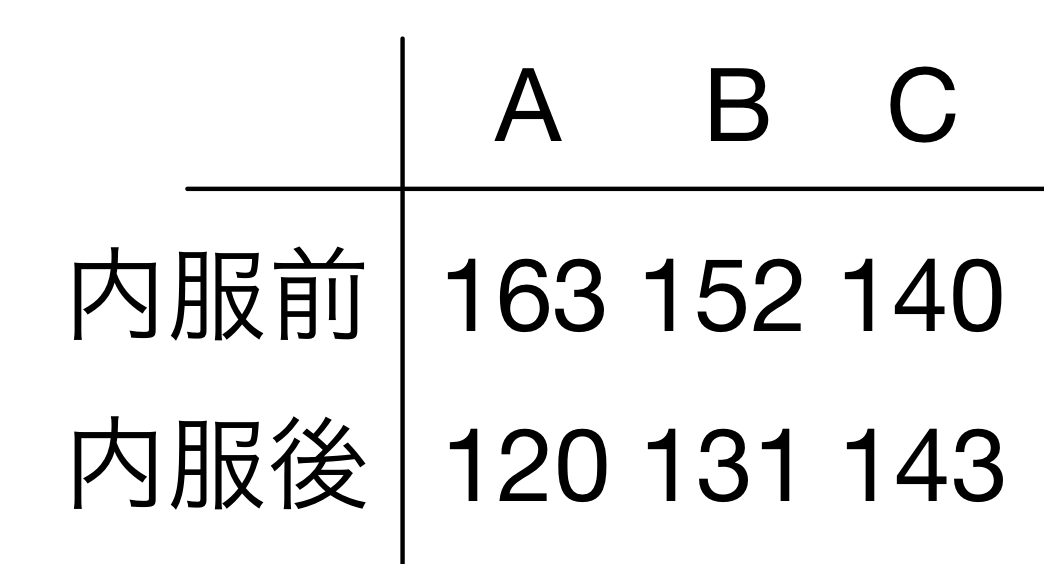
3人の被験者に対して、降圧剤を内服前後の収縮期血圧の変化を見てみると以下の表のようになりました。これに対してウィルコクソンの符号付き順位検定をしてみます。帰無仮説は前後の差はなく、いずれの分布関数の中央値も同じかつ中央値に対して対称、と考え、5%を有意差とする片側検定を行います。

f:id:medibook:20210224052014j:plain

まずは、データの差の大きさの順位とその正負を確認します。

f:id:medibook:20210224052047j:plain

すると、こうなりました。

次に検定統計量である差が正である順位の和 $W_n$ を求めます。

$W_n=3+2=5$

続いて、この順位の和の組み合わせを全て考えてみると以下のようになります。

{0}

{1}
{2}
{3}
{1,2}

{1,3}

{2,3}

{1,2,3}

以上の8通りです。

帰無仮説において、この組み合わせはいずれも同じ確率で出現するはずです。

この中で、先程の検定統計量 $W_n=5$ より大きいのは

{2,3}

{1,2,3}

の2パターンなので、求める確率は

$P(W_n\gt5)=2/8=0.25$

となり、有意差がないことがわかりました。

ウィルコクソン符号付き順位検定の一般的な式

一般化して考えると、まずデータから得られた変化後の確率変数Xは未知の分布関数F(X-Δ)に従うと考えます。Δに対して分布関数は対称な形をしていることを仮定します。

変化前の確率変数 $\Delta_0$ について

$H_0: \Delta_0=\Delta\\H_1: \Delta_0\neq\Delta$

として検定を行います。（両側検定の場合）

検定の式としては

$P(W_n\gt w_n)=\sum_{i=1}^niV_i$

となります。

データの数をnとし、データの差 $Z_i$ を順序統計量として順位(i)に応じて並べます。大きい方から $Z_n\gt Z_{n-1}\gt....Z_1$ という順番です。 $V_i$ はデータの正負を指示するための定義関数で

$V_i=1$ （ $Z_i$ が正のとき）

$V_i=0$ （ $Z_i$ が負のとき）

と定義されます。

サンプル数が多い場合の正規近似

符号検定と同様にこちらもサンプル数が多ければ正規近似ができます。

そこで必要になるのが検定統計量の平均と分散です。

帰無仮説において $V_i$ は1/2の確率で正負となるベルヌーイ分布と言えることを利用して、平均は

$E[W_n]=\sum iE[V_i]\\=\frac{1}{2}\sum i\\=\frac{n(n+1)}{4}$

分散は

$Var(W_n)=Var(\sum iV_i)\\=\sum Var(iV_i)\\=\sum i^2Var(V_i)\\=\frac{1}{4}\sum i^2\\=\frac{n(n+1)(2n+1)}{24}$

となります。

よってサンプル数が大きいとき標準正規分布で近似すると

$Z=\frac{w_n-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}$

と言えます。

参考文献：

リンク

FOLLOW

コメントを残すコメントをキャンセル

認知症の新薬aducanumabの話が不穏すぎるので、製薬関連の本をいくつか読んでみた

【統計応用・医薬生物学】ノンパラメトリック法・符号検定【統計検定1級対策】