引き続きまして『入門統計学的因果推論』の第2章を読み進めてみます。ここからは具体的なグラフィカルモデルの応用になってきます。
目次:
条件付き独立と条件付き従属について考える意義
ここからは前回説明したSCMおよびグラフィカルモデルにおいて各変数が条件付き独立なのか従属なのかをどのようにして考えるか説明していきます。
その前になぜ、条件付き独立や従属が大事なのか。
本書の冒頭でも触れられているようにいわゆる「シンプソンのパラドックス」において、全体をみるか、層別化してみるかを考えたいとき、この考え方が必要になってきます。
観察研究において何らかの介入の効果を考えたいときは交絡因子の影響を取り除きたいのが通常です。
例えば、ある薬を内服するかどうかが、ある病気を治癒するのに役立つかどうかを考えてみます。健康的な生活習慣で真面目な人は、薬の内服もしやすいし、病気も治癒しやすいとしてみましょう。グラフィカルモデル風に考えると以下のようになります。
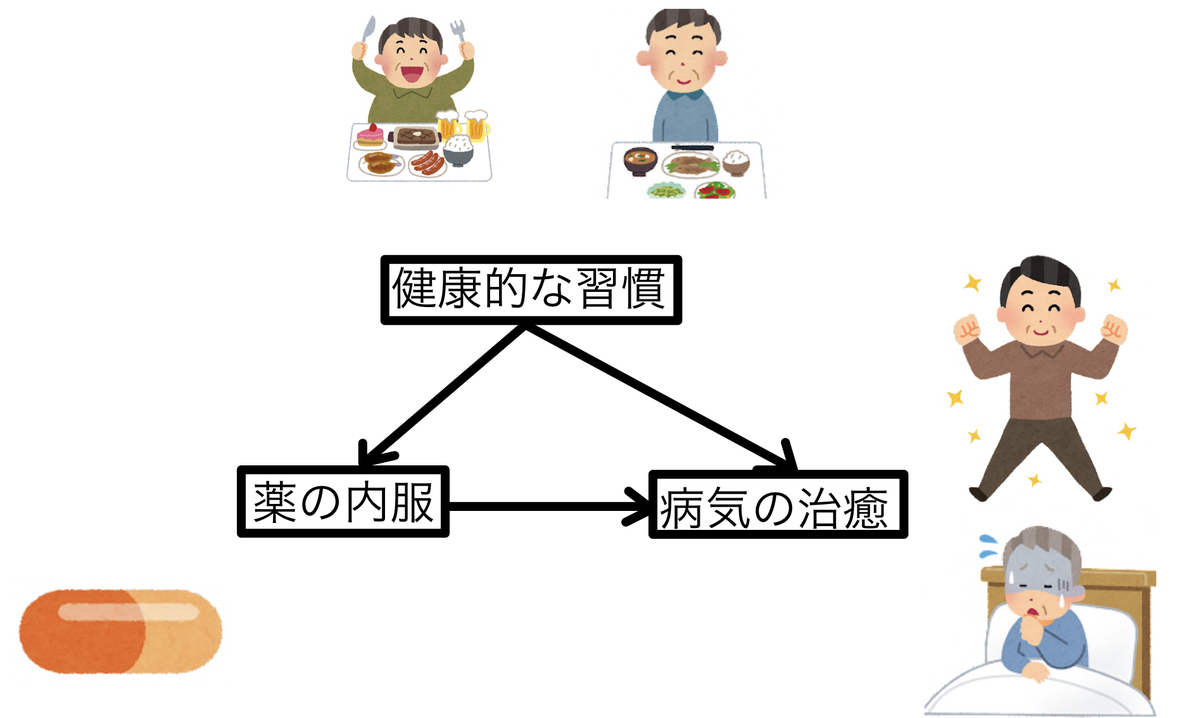
この時、薬の効果を純粋に考えるには交絡因子である「健康的な生活習慣」の影響を取り除かなければいけません。単純に薬の内服あり・なしで結果を出すと内服のある人は健康的な生活習慣をしている可能性が高いため、病気の治癒の効果もさらに上乗せされて見えてしまうからです。
つまり、「薬の内服」と「健康的な生活習慣」を独立の関係にしなければいけないわけです。
そのための答えは「健康的な生活習慣をしているかどうかで層別化する(条件付け)」ことになります。こうすることで初めて純粋な薬の効果を推定することができます。
よって、どれを条件付けするとどの変数が従属あるいうは独立になるのか、ということが重要になります。グラフィカルモデルの形によってその規則性は色々とあり、今回順番に確認していきます。また従属・独立の定義はそもそも何なのかも改めて見ていきます。
独立と従属の式における定義
SCMにおいては独立・従属あるいは条件付き独立・従属ということを式で表すことができます。これがグラフィカルモデルでは見ただけでわかるようになっていますので、利点の一つとなっています。
まずSCMにおける独立・従属がどのように表されるかみていきます。
SCMで“変数XとYが独立である“とは次のような定義が当てはまります。
つまり、Yがどのような数で条件付けされようが、Xがとる値の確率にはなんら影響を及ぼさないということですね。
逆に、“XとYが従属である”場合は
となるようなyが存在する、ということになります。
また、あるもう一つの変数の条件付けの下で、二つの変数が独立あるいは従属になる場合があります。“Zの条件付けの下でXとYが独立である”という場合は
と表すことができます。
では、どのようなグラフィカルモデルだと従属・独立あるいは条件付き従属・独立になるのか。そのパターンをそれぞれ見ていきます。
連鎖経路(chain)

まず連鎖経路(chain)と呼ばれるのはこのように連なった形をしているものを指します。この時、XとYとZはそれぞれ有向道で繋がっており従属の関係にあるのはすぐ分かりますが、大事なのは条件付きにした時どうなるか、ということです。
結論から述べれば、連鎖経路ではXとZの間にあるYが条件付けされると独立となります。
例えば、親の年収(X)がどの大学へ行くか(Y)に影響し、どの大学に行くか(Y)がどの企業に就職するか(Z)に影響すると仮定してグラフィカルモデルを書くとしましょう。親の年収(X)はどの企業に就職するか(Z)には直接影響しないという前提です。
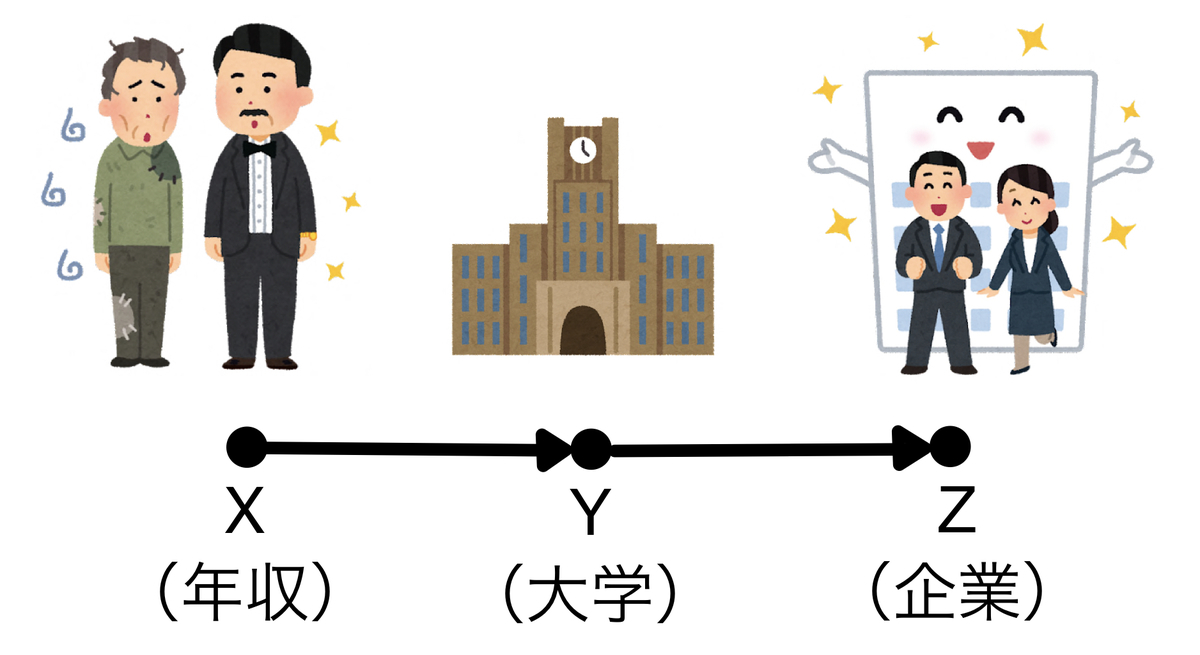
そうすると、どの大学に行くかを固定すれば(条件付け)どの企業に就職するかは自ずと決まってきます。つまり、親の年収(X)と就職先の企業(Z)が独立となるわけですね。
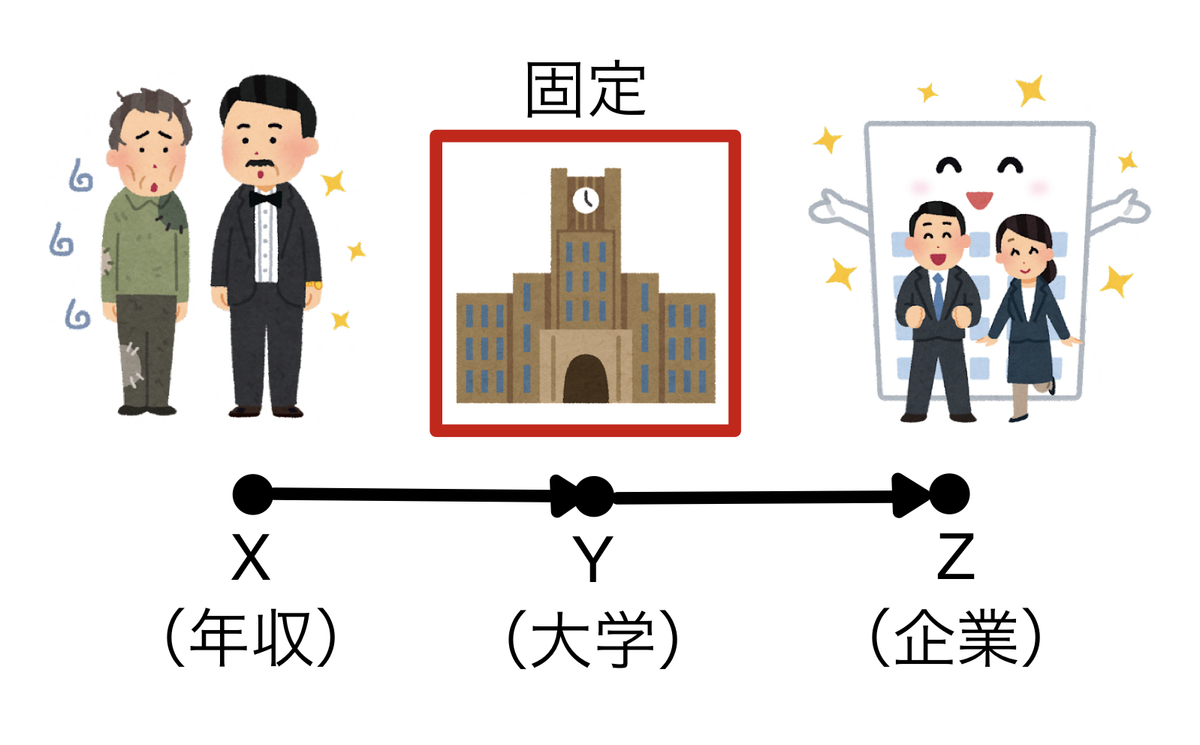
これと同様にグラフィカルモデルの形によって、どうしたら条件付き独立・従属となるかが規則的に決まってきます。
分岐経路(fork)
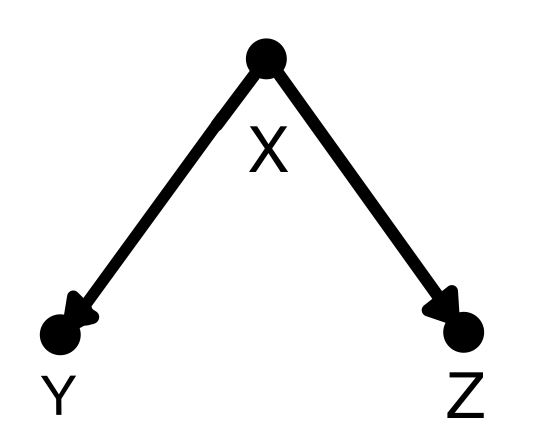
分岐経路(fork)はこのように二股に分かれる形を指します。この場合は分岐点であるXで条件付けすると分かれた先のYとZは互いに独立、条件付けしなければYとZは従属となります。
例えばある心疾患(Y)と脳疾患(Z)は直接的には関連しないものとしましょう。
どちらも運動習慣(X)があると発症しにくくなると考えてみます。グラフィカルモデルはこんな風です。
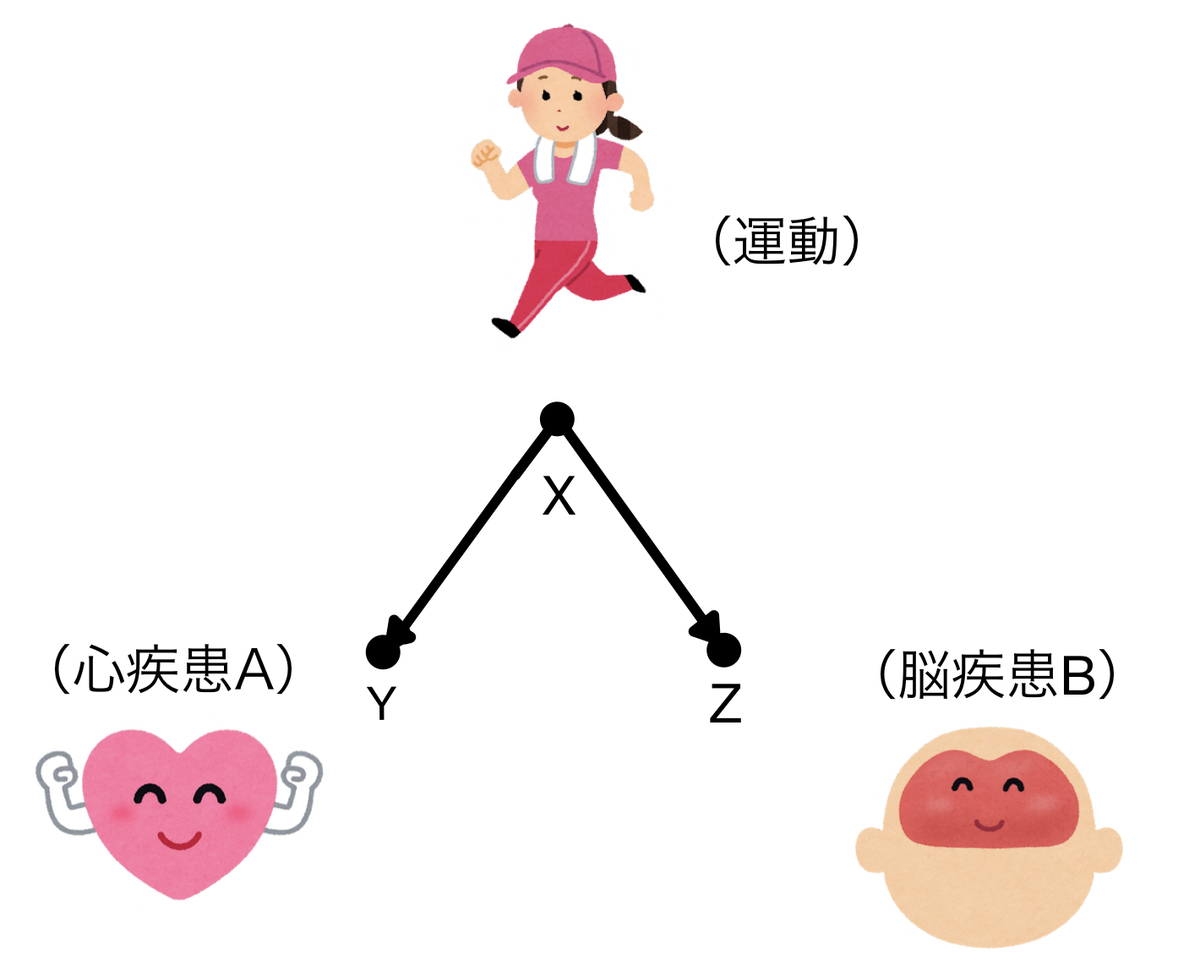
運動習慣のある人は心疾患も脳疾患も発症しにくく、運動習慣のない人は心疾患も脳疾患も発症しやすくなります。そうすると心疾患の発症しやすさが脳疾患の発症しやすさとまるで連動しているように見えます。つまり二つは従属の関係に見えるわけです。
ところが、ここで運動習慣のあるなしを固定すると、運動習慣以外にはそれぞれ独立した要因からしか影響を受けていないのため、二つの疾患は独立となります。これがfork
合流点(collider)
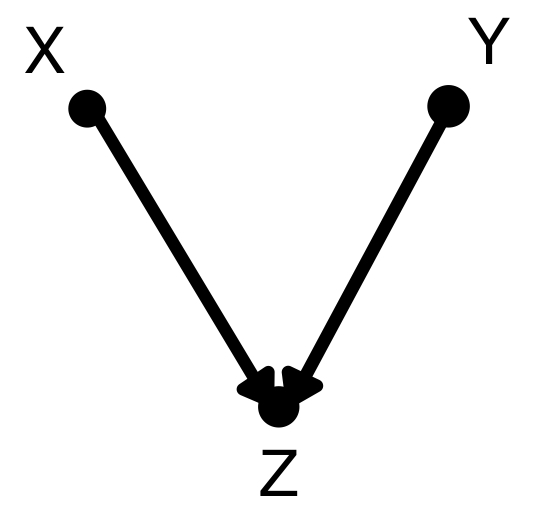
合流点(collider)はこのように二つの点が一つの点で合流します。Zで条件付けされたときXとYは従属、条件付けされないときはXとYは独立となります。forkの場合の逆ですね。
今度は例として遺伝的要因(X)と環境要因(Y)が原因となる肺疾患(Z)を考えてみましょう。
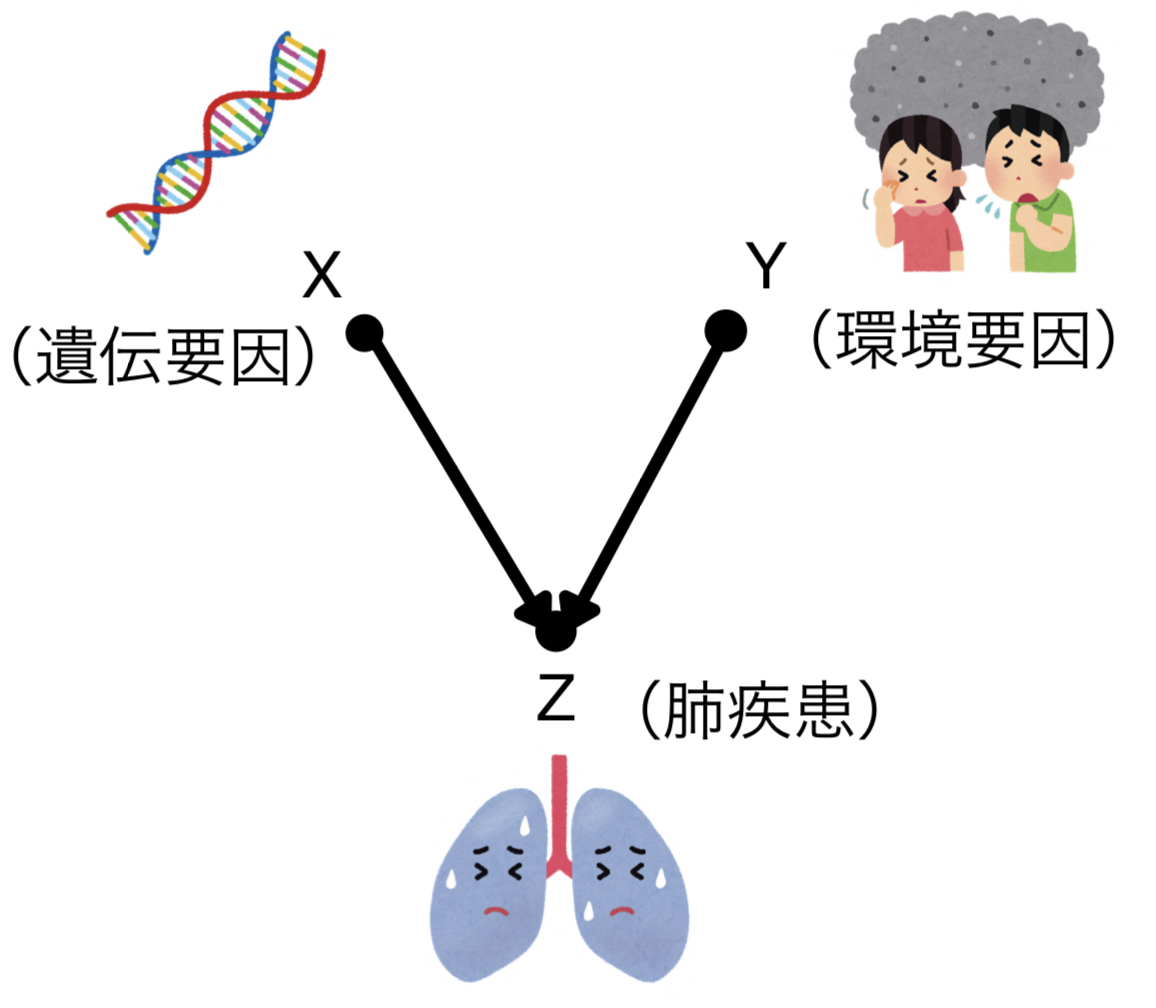
肺疾患について何の条件付けもなければ、当然ながら遺伝要因と環境要因は関係しません。不思議なことに肺疾患について条件付けをするとこの二つが従属となるのです。なぜでしょうか。
肺疾患がある人に限って考えてみたとき、例えば遺伝要因があまりなかったとします。そうすると必然的にもう一つの原因である環境要因の影響は大きいはずです。つまり、遺伝要因が小さくなることによって環境要因は大きくなってしまうわけです。従属の関係にあることがわかります。
逆もまた然りですので、以上のことから合流点について条件付けするとその原因同士は従属となります。
d-分離(d-separation)
これらの原則を用いると複雑なグラフであっても、2つのノードが独立であるかどうかを判断することができます。
あるノードの集合Zの条件が与えられた下でX,Yの二つのノードの独立となるならば「Zが与えられた下でX,Yはd-分離(d-separation)とされている」あるいは「Zによりブロックされている」と言われます。なお、d-分離のdはdirectionalを意味しているようです。
本書では従属性を水の流れのように例えて、あるノードとノードの間の道pがZによりブロックされると従属性が流れず、それぞれは独立となる、というように説明されています。
具体的な例がないとわかりづらいのでみてみましょう。
例えば下記のようなグラフィカルモデルを考えてみます。
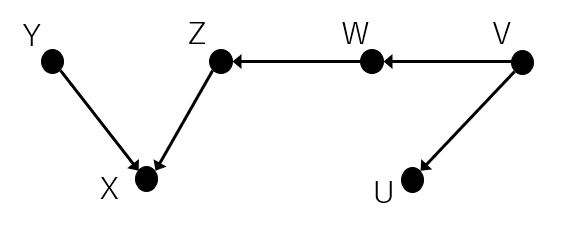
ある程度複雑な構造をしてますね。
この時YとUの関係はどうなっているでしょうか。それぞれ部分に分けてみていきます。
①Y、X、Zの関係は上記のcolliderに当てはまるため条件付けがなければYとZは互いに独立です。
②Z、W、Vは上記のchainなので条件付けがなければZとVは従属です。
③W、V、Uは上記のforkなので条件付けがなければWとUは従属です。
何も条件付けがない場合、①からYとZが独立であるため、従属性の流れはそこでブロックされます。よって、YとUはそれぞれ独立となります。逆にXのみ条件付きであれば、そこを従属性が流れるためYとUは従属となります。
ところが、Xに加えてWが条件付きとなるとどうでしょう。
そうなるとWによって従属性はブロックされます。よって、YとUは独立となります。
このように何を条件付けしたら何が周辺独立となるかが簡単に判断できることはDAGの利点となっています。
さて、ここまで読んできて紹介したモデルは簡単な例が多いです。
・疾患はそんなに単純な要因だけじゃないのではないか
・介入試験とかはどう考えれば良いのか
と思うわけですが、そこについては次の3章の内容となってくるので引き続き読み進めていきます。













コメントを残す