さて、大学院の授業でBox Muller法(あるいはBox Muller変換)が出てきたのでまさにそれを証明する問題である現代数理統計学の基礎の4章問8を解いてみます。
おまけとして三角関数の計算を使わないMarsaglia polar法の紹介とC とPythonでのコードも書いてみようと思います。
2022年の統計検定1級問2はこの辺にも関連しうる問題だったので、こういった話は知っておいて損はないかもしれません。(と後から気づきました)
まずはBox Muller法の証明から。
Box Muller法
まず区間(0,1)とする一様分布U1,U2を準備します。
ここで
\(r=\sqrt{-2logU_1}, \theta=2\pi U_2\)
とします。
そこで確率変数X,Yを
\(X=rcos\theta, Y=rsin\theta\)
とすれば、X,Yはそれぞれ独立に分布する標準正規分布となります。
証明
2変数の変数変換を使っていけばできます。
ただし、逆三角関数の微分が必要となるのであらかじめ紹介しておきます。
\(\frac{d}{d\theta}tan^{-1}\theta=\frac{1}{1+\theta^2}\)
使うのはこれだけです。
ではまず、U1,U2とX,Yの関係を整理します。
\(-2logu_1=r^2=x^2+y^2\)
よって
\(u_1=e^{-\frac{x^2+y^2}{2}}\)
また
\(2\pi u_2=\theta=tan^{-1}\frac{y}{x}\)
よって
\(u_2=\frac{1}{2\pi}tan^{-1}\frac{y}{x}\)
となります。
あとはそれぞれを微分してヤコビアンJを計算します。
\(J=|-xe^{-\frac{x^2+y^2}{2}・\frac{x}{2\pi(x^2+y^2)}}-ye^{-\frac{x^2+y^2}{2}・\frac{y}{2\pi(x^2+y^2)}}|\\=\frac{1}{2\pi}(\frac{x^2}{x^2+y^2}e{-\frac{x^2+y^2}{2}}+\frac{y^2}{x^2+y^2}e{-\frac{x^2+y^2}{2}})\\=\frac{1}{\sqrt{2\pi}}e^{\frac{x^2}{2}}・\frac{1}{\sqrt{2\pi}}e^{\frac{y^2}{2}}\)
となります。ほぼ答え出てますね。
独立した標準正規分布同士の同時分布がキレイに出ています。
最後に変数変換のためU1、U2の同時分布とヤコビアンの積を出しますが、U1,U2はどちらも一様分布のため
\(f(u_1)=g(u_2)=1\)
であり、同時分布も1なので、最終的な結果としては
\(f(x,y)=1・\frac{1}{\sqrt{2\pi}}e^{\frac{x^2}{2}}・\frac{1}{\sqrt{2\pi}}e^{\frac{y^2}{2}}\)
となり、X,Yはそれぞれ独立に分布する標準正規分布であることが証明できました。
Marsaglia polar法
機器によって三角関数の計算に時間を要する場合に「三角関数を計算せずに標準正規分布を作り出そう」というのがMarsaglia polar法です。
PCでの計算方法の実際について大して詳しくないのでわかりませんが英語版wikipediaを見ると計算方法によって、Box Muller法とどっちが早いか議論が分かれるようです。ちなみに自分のPCでやったところ、Box Muller法のほうが結局早い気がしましたが、、、。
やっていることは基本的にBox Muller法と同じなのですが、乱数の出し方が異なります。
証明
こちらでは
w,zを区間(-1,1)とする一様分布とします。
その中から原点を中心とする半径1の単位円に入ってものを使い、そうでないものを棄却します。計算機によってはここのステップが少し時間がかかるようです。
そこで
\(s^2=w^2+z^2\)
とします。
するとこの\(s^2\)は区間(0,1)として一様分布になるため、これを用いて先ほどの
\(\sqrt{-2logU_1}\)
を得ます。
さらにwとzを半径sで割ればこれらも一様分布となるため
\(\frac{w}{s}=cos2\pi U_2\\\frac{z}{s}=sin2\pi U_2\)
となります。
こうすれば、三角関数の数値を計算するというステップを踏まずに、必要な乱数を得ることができます。
C++ とPythonで実装
ここからは最近ようやく勉強し始めたプログラミングコードで実際にやってみます。ただの初心者なので、自習を兼ねて。まずはボックスミュラー法から。
Box-Muller法
コードは以下のようにしました。datファイル形式で繰り返し回数と正規乱数が出力されます。
#include <iostream>
#include <fstream>
#include <cmath>
#include <time.h>
#include "MT.h" //MT.hのある絶対パスあるいは相対パスを入力
using namespace std;
double generate()
{
double u1 = genrand_res53(); //[0,1)の一様実乱数
double u2 = genrand_res53();
double z1 = sqrt(-2.0 * log(u1)) * cos(2.0 * M_PI * u2);
//double z2 = sqrt(-2.0 * log(u1)) * sin(2.0 * M_PI * u2); z2は計算不要なのでコメントアウト
return z1;
}
int main()
{
init_genrand(time(NULL));
char fname[128];
sprintf(fname, "normal_distribution10.dat");//任意のファイル名を入力
ofstream file(fname);
for (int i = 0; i < 10; i++) {
double normal_distribution_sample = generate();
file << i << " " << normal_distribution_sample << endl;
cout << "Sample " << i << ": " << normal_distribution_sample << endl;
}
//繰り返し回数は10回
file.close();
return 0;
}乱数生成にはメルセンヌツイスタと呼ばれる疑似乱数を用いています。MT.hのファイルを入手して、適宜必要なフォルダに入れてパスを入力する必要があります。乱数生成の精度は方法により変わるようで、こちらのサイトが参考になります。
同様の乱数生成を用いて、Marsaglia polar法も見ていきます。
Marsaglia polar法
こちらは以下のようなコードにしました。
#include <iostream>
#include <fstream>
#include <cmath>
#include <time.h>
#include "MT.h"//絶対パスまたは相対パスを入力
using namespace std;
double generate()
{
double w,z,s;
do {
w = genrand_res53()*2-1;
z = genrand_res53()*2-1;
s=w*w+z*z;
}while(s>=1.0 || s==0.0);//これによって単位円の外にある点およびs=0を除外する
double x = sqrt(-2.0 * log(s)) * (w / sqrt(-2.0 * log(s)));
return x;
}
int main()
{
init_genrand(time(NULL));
char fname[128];
sprintf(fname, "mnormal_distribution10.dat");
ofstream file(fname);
for (int i = 0; i < 10; i++) {
double normal_distribution_sample = generate();
file << i << " " << normal_distribution_sample << endl;
cout << "Sample " << i << ": " << normal_distribution_sample << endl;
}
file.close();
return 0;
}While文を使って単位円に入らない点を棄却します。乱数生成の方法は同様ですが、こちらは一様分布の区間が[-1,1]となっています。
さて、最後に作った正規乱数をヒストグラムでみてみます。描画はpythonのmatplotlibを使います。
import matplotlib.pyplot as plt
import numpy as np
# データ読み込み
data = np.loadtxt('先ほど作ったデータのパス名', usecols=[1])
# ヒストグラムの作成
plt.hist(data, bins=100, density=True)
# 理想的な正規分布の曲線を表示
x= np.linspace(-6, 6, 100)
f= (2.*3.14)**(-0.5)*np.exp(-x**2./2.)
plt.plot(x,f, "-",markersize=3,linewidth = 2.0, color="k",label=r"$\frac{1}{\sqrt{2\pi}}e^{-X^2/2}$")
# 軸ラベルの設定
plt.xlabel('x')
plt.ylabel('count')
# グリッド線を表示
plt.grid(True)
# グラフの表示
plt.show()1000個の正規乱数で実行してみたところ以下のような図が得られました。
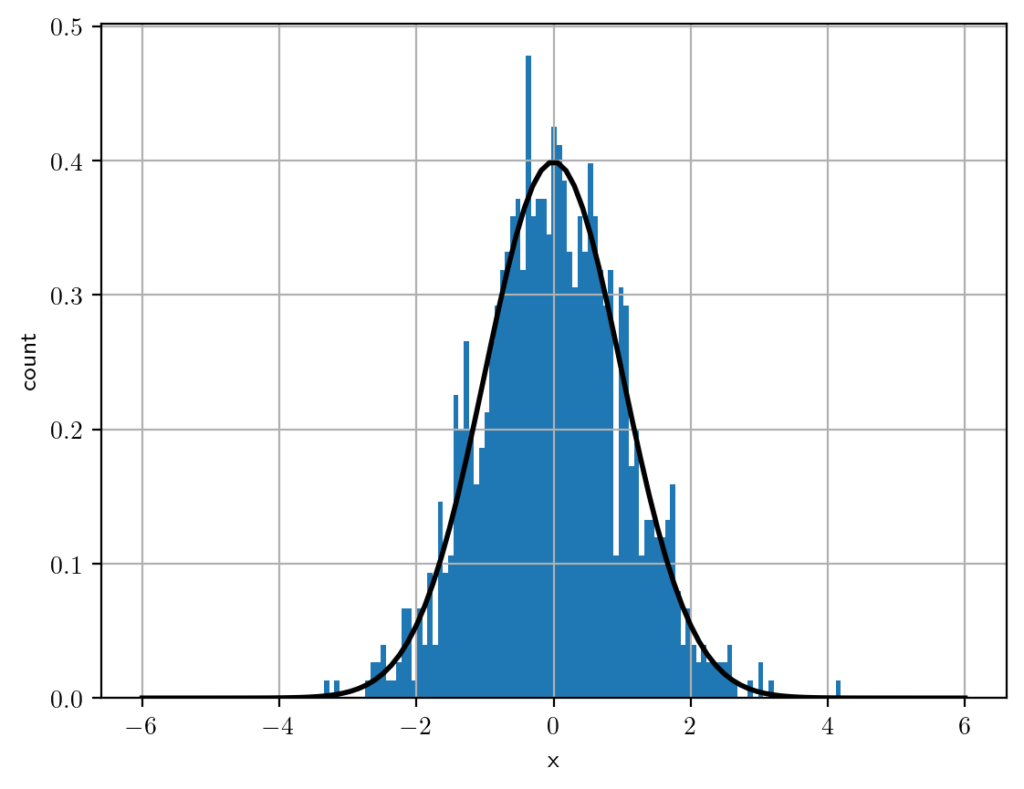
若干外れているところがありますが、まあまあそれっぽい形にはなってますね。
ChatGPT先生のおかげでプログラミングに対する障壁がだいぶ下がったので、これからはバシバシ利用していきたいと思います。
















コメントを残す