※ブログ記事の商品・サービスリンクにはアフィリエイトリンクが含まれます。

現代数理統計学の基礎　5章　問1

統計学の自学自習のためにここ1年ほど

「現代数理統計学の基礎　久保川達也著」

という本を使っています。

統計検定1級合格者のブログなどをみていると

”これをやればほぼ範囲は網羅されています”

と書いてあるので1冊マスターしようという気持ちで買ったのですが

いかんせん難しい。

そんなわけで、ほかの解説書もみながらやっているんですけども

同じようにつまずくひとが沢山いるのか

googleの検索ワードをみると”現代数理統計学の基礎　難しい”

とか”現代数理統計学の基礎　解説”とかいうワードが並びます。

何度か読み直してみるとやっぱり良い本だなと思ったりもするのですが

そこにたどり着くのに苦労するのと、練習問題の解説が

たまに行間を飛ばしていてわからん、、、ということがあります。

そこで自分の書いた解答を復習がてら並べてみることにします。

専門ではないゆえに間違ったことがあるかもしれないので

詳しい方がいたらぜひ突っ込みをお願いします。

実際1～3章あたりはすでに解説を書いておられるブログもありそうなので

飛ばして、5章から書きます。

ちなみに数式ですが、コードを打ち込んで書くべきなんでしょうけれど

正直時間がかかって面倒くさいので手書きをスキャンしたものにします。

字が汚くてすみません、、笑

（※2021.03.12追記　コメントで誤りを指摘していただいたので修正してLatexに直しました、ありがとうございます）

第5章　問1

標本平均と標本分散×n1/2乗の平均と分散を求める問題。

第5章のp87で示されていたように標本平均と標本分散の独立性と

標本平均の分布の標準化、下図Yがχ2乗分布に従うことを利用して解きます。

まずは期待値から

$Z=\frac{\sqrt n(\bar X-\mu)}{\sigma}, Y=\frac{nS^2}{\sigma^2}$ とおくと

$Z\sim N(0,1), Y\sim\chi_{n-1}^2$

となります。

確認ですがχ2乗分布はガンマ分布に含まれるもので

自由度nのχ2乗分布はGa(n/2, 2)でした。よって今回はGa((n-1)/2, 2)と言えます。

これを用いて期待値を計算します。

$E[\bar X-\sqrt nS]=\frac{\sigma}{\sqrt n}E[Z]+\mu+\sigma E[\sqrt Y]$

このうち $E[\sqrt Y]$ は

$E[\sqrt Y]=\int_0^{\infty}y^{\frac{1}{2}}\frac{1}{\Gamma(\frac{n-1}{2})}(\frac{1}{2})^{\frac{n-1}{2}}y^{\frac{n-1}{2}-1}exp(-\frac{y}{2})dy\\=\int_0^{\infty}\frac{1}{\Gamma(\frac{n-1}{2})}(\frac{1}{2})^{\frac{n-1}{2}}y^{\frac{n}{2}-1}exp(-\frac{y}{2})dy\\=\frac{1}{\sqrt2\Gamma(\frac{n-1}{2})}\int_0^{\infty}(\frac{y}{2})^{\frac{n}{2}-1}exp(-\frac{y}{2})dy\\\frac{1}{\sqrt2\Gamma(\frac{n-1}{2})}(\frac{1}{2})^{\frac{n}{2}}\int_0^{\infty}(u)^{\frac{n}{2}-1}exp(-u)2du\\=\frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})}\sqrt2$

ガンマ分布は上手く変数を中に入れ込んでしまえば

ガンマ関数が作れるので答えがでます。

最後はu=y/2として置換しました。

これとE[Z]=0を代入して

$E[\bar X-\sqrt nS]=\frac{\sigma}{\sqrt n}E[Z]+\mu+\sigma E[\sqrt Y]\\=\mu+\sqrt2\sigma\frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})}$

続いて分散は

$Var(\frac{\sigma}{\sqrt n}Z+\mu+\sigma\sqrt Y)\\=\frac{\sigma^2}{n}Var(Z)+0+\sigma^2V(\sqrt Y)\\=\frac{\sigma^2}{n}+\sigma^2V(\sqrt Y)$

定数項は分散を取ると0になることと、ZとYが独立であることを利用してこのように変形します。

続いて $\sqrt Y$ の分散は

$Var(\sqrt Y)=E[Y]-(E[\sqrt Y])^2\\=n-1-2\{\frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})}\}^2$

となります。Yの期待値はカイ二乗分布の期待値なので自由度に一致し、n-1となります。

以上を先程の式に代入すれば答えが出ます。

3件のコメント

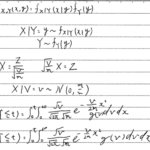
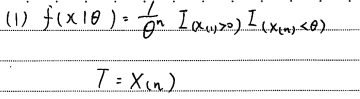
大阪で整形外科の医師をしているものです．tosuke先生の解説は大変に分かりやすく，感服しております．ありがとうございます．
ちょっと気になったところがあったので，コメントさせていただきます．私の方が間違っていたらご指摘いただきますと幸いです．
現代数理統計学の基礎第5章問1
期待値のところ
　ZとYの独立性は特に必要ないような気がします．
ガンマ関数に見立てるところ
　4つ目の「＝」の定積分した部分はは2Γ(n/2)になるかと思います．y/2のままでガンマ関数にみるとすると積分変数がdyのままなので合わないと思います．最後の答えに関しては結果的に√2が分子にくるように思います．
分散のところ
　ZとYが独立であることを利用して，最初の和の分散を分散の和にしてから計算したほうが早くて計算量が少ないような気がします．

返信

＞show55さん
もったいないコメントを頂きまして恐縮です。全てご指摘頂いた通りだと思いますので、修正させていただきました。ご指摘有難うございます。
show55さんは臨床医でありながら数理統計にも造詣が深いように感じられますが、普段どのように、どんな機会で勉強されているのでしょう。差し支えない範囲で構いませんが、今後の参考の為にも教えて頂けますでしょうか？

返信

こちらこそお返事いただいてしまって驚いています．
臨床医学の論文を書く際に対応する部分を少し調べたり，Rのコードを書いたりして勉強してきました．そうこうしているうちに，もうちょっとしっかりと知識を整理したいと思ったのと，自分の専門分野の中では対外的なアピールになるかと思いまして統計検定1級の勉強を始めました．始めてみましたら，自分は統計の「統の字の糸へん」の最初の1画すらわかっていないことがわかりました(笑)．
tosuke先生の方法と似ていますが，久保川本をメインに数理統計を趣味がてら勉強しています．もし，メールで連絡いただけましたら，もうちょっと率直にお話しできると思っています（差し出がましかったらすみません）．
今後も先生のブログを参考にさせていただきます．

返信