さて、ほとんどの地域で警戒宣言も解除され、徐々に普段の生活に戻りつつある今日この頃ですが、我が家は第二子が生まれたこともあって、最近はひたすら三食の準備と家事と上の子の散歩に日々追われております。
今日はなんと上の子が夕方ごろに急に寝てしまったので、久々の更新。(と思ったら夜書いている途中に起きてきて「おなかすいた、、、」と結局中断。そりゃお腹すくよね。)
あまりに集中して何かに取り組む時間が取れないので、現実逃避気味でしたが、そろそろ統計検定1級に向けた勉強を再開したいと思います。
統計数理の問題を解いていると時折マクローリン展開を使う問題や証明に出会うのですが、時たま会う、というくらいでイマイチ使い方を忘れがちです。そこで、マクローリン展開を使う証明についていくつか復習してみたいと思います。
マクローリン展開とは
一言でいえば関数f(x)の近似式です。とても簡単で扱いやすいため色々な証明や問題を解くのに使われます。
式としては
\(f(x)=f(0)+f'(0)x+\frac{f”(0)}{2!}x^2+\frac{f”'(0)}{3!}x^3+…\)
と続きます。
この証明や簡単な例については分かりやすいサイトが多数あるので割愛します。
以下、いつも通り「現代統計数理学の基礎」を参考にして、一部詳細加えつつ、マクローリン展開の統計数理学での活用事例をみていきます。
活用例1:負の二項分布
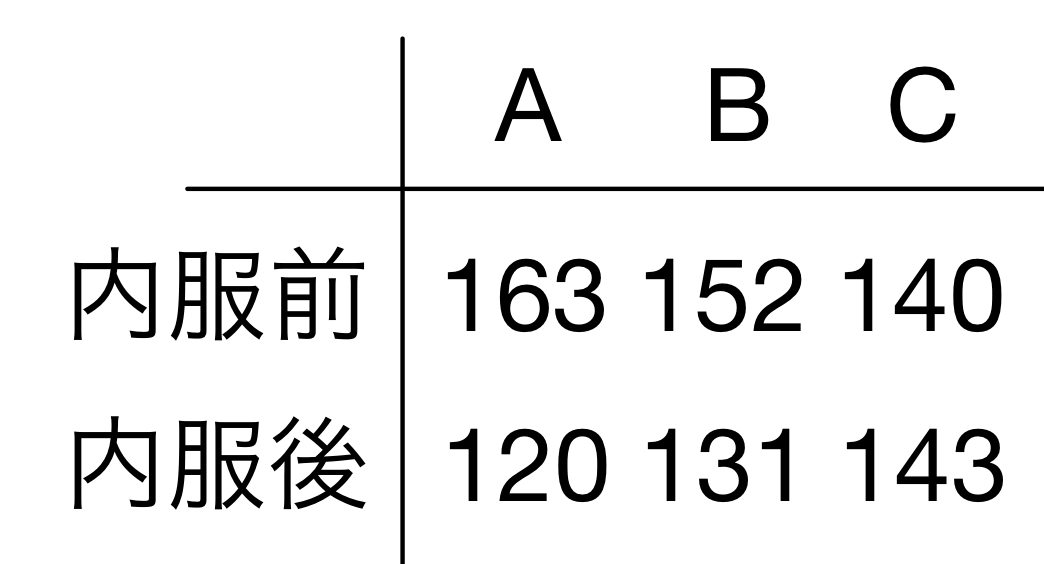
成功確率をpとするベルヌーイ分布(成功か失敗しかない試行)についてr回成功するまでに要した失敗xの数がとる分布を「負の二項分布」と呼びます。
分布を表す式としては
\(P(X=x)=_{r+x-1}C_xp^r(1-p)^x\)
です。
この分布の確率母関数やモーメント母関数を表すのにマクローリン展開が使われます。ネット上でこれらの導出方法を調べると、「負の二項分布の全確率が1になる」ことを利用したものもありますが、「負の二項分布の全確率が1になる」ということ自体、マクローリン展開で証明したりしているので、結局はマクローリン展開は絡まざるを得ないとは思います。
ということで負の二項分布の全確率が1になることを証明します。
成功する確率 \( p \) に対して、失敗する確率を \( q \) とすると
\( 1 – q = p \) となります。
マクローリン展開を使って
\( \frac{1}{1 – q} \) を考えると
\( f(q) = \frac{1}{1 – q}, f'(q) = \frac{1}{(1 – q)^2}, f”(q) = \frac{2}{(1 – q)^3}, f”'(q) = \frac{2 \cdot 3}{(1 – q)^4} \)
となっていくので、それぞれ0を代入して
\( \frac{1}{1 – q} = 1 + q^2 + q^3 + q^4 + \dots = \sum_{k=0}^\infty q^k \)
となります。
ちょうどマクローリン展開で出てくる分母の階乗が、微分で出てくる階乗にキャンセルされる形となるんですね。
この式はちなみに高校で習う無限等比級数の和の公式の逆となっていることが分かります。初項 \( a \) で比 \( r \) の等比数列の和が \( \frac{a}{1 – r} \) というやつですね。
あとはちょっとテクニカルですが、これを両辺で \( q \) に関して微分していくと
\( \frac{1}{(1 – q)^2} = \sum_{k=0}^\infty k q^{k – 1} = \sum_{k=1}^\infty k q^{k – 1} (k=0 の項は 0 になるため) = \sum_{k=0}^\infty (k + 1) q^{k} \)
これを \( r – 1 \) 回繰り返せば最終的な目標の式に近づきます。
\( \frac{(r-1)!}{(1 – q)^r} = \sum_{k=0}^\infty (k + r – 1) \dots (k + 1) q^{k} \)
よって
\( 1 = \sum_{k=0}^\infty \frac{(k + r – 1) \dots (k + 1) q^{k} (1 – q)^r}{(r – 1)!} \)
となり \( k \) を \( x \) に、\( q \) を \( 1 – p \) に直し
\( (x + r – 1) \dots (x + 1) = \frac{(x + r – 1)!}{x!} \)
であることを使えば
\( 1 = \sum_{k=0}^\infty \frac{(x + r – 1) \dots (x + 1)(1 – p)^{x} p^r}{x! (r – 1)!} \)
となり証明できました。
活用例2:スターリングの公式
ガンマ関数の近似を得るための公式です。 \( k \) が十分に大きいとき、以下の近似式が成り立ちます。
\( \Gamma(k + a) \approx \sqrt{2 \pi} k^{k + a – \frac{1}{2}} e^{-k} \)
また、ガンマ関数は階乗の一般化(整数 \( n \) 以外に拡張したもの)なので、上記の式に
\( a = 1 \) を代入することで
\( \Gamma(k + 1) = k! \approx \sqrt{2 \pi} k^{k + \frac{1}{2}} e^{-k} \)
となります。
証明も色々あるようですが、参考文献のやり方に従ってやってみます。
まずガンマ関数の定義に従うと
\( \Gamma(k + a) = \int_{0}^{\infty} x^{k + a – 1} e^{-x} dx \)
ここで \( x = k + \sqrt{k} z \) と変数 \( z \) に変換します。
\( dx = \sqrt{k} dz \) なので
\( \Gamma(k + a) = \int_{-\sqrt{k}}^{\infty} (k + \sqrt{k} z)^{k + a – 1} e^{-k – \sqrt{k} z} \sqrt{k} dz \)
変数 \( z \) 以外の部分を外にくくりだします。
\( k^{k + a – \frac{1}{2}} e^{-k} \int_{-\sqrt{k}}^{\infty} \left(1 + \frac{z}{\sqrt{k}}\right)^{k + a – 1} e^{-\sqrt{k} z} dz \)
ここでようやくマクローリン展開を使うことになりますが
積分の中身について使用します。
\( \log\left(1 + \frac{z}{\sqrt{k}}\right) = 0 + 1 \cdot \frac{z}{\sqrt{k}} – \frac{1}{2!} \left(\frac{z}{\sqrt{k}}\right)^2 + \dots \)
よって、近似したときに積分の中身に戻したときに残るのは \( \exp\left\{-\frac{z^2}{2}\right\} \) のみとなります。
最初の式に戻ると
\( k^{k + a – \frac{1}{2}} e^{-k} \int_{-\sqrt{k}}^{\infty} \exp\left\{-\frac{z^2}{2}\right\} dz \)
\( -k \) は十分に大きいのでガウス積分と同様になって
\( = k^{k + a – \frac{1}{2}} e^{-k} \sqrt{2 \pi} \) となります。
活用例3:デルタ法
確率変数 \( X \) の期待値 \( E[X] \) は分かるけれど、 \( X \) を変数変換した \( Y = g(X) \) の期待値 \( E[g(X)] \) が求めにくい場合などに用いられる近似式です。これはマクローリン展開ではなくテイラー展開ですが。
\( E[X] = \mu \) として \( \mu \) 周りのテイラー展開をすると
\( g(X) \approx g(\mu) + (x – \mu) g'(\mu) + \frac{1}{2} (x – \mu)^2 g”(\mu) \dots \)
となります。
平均の場合、期待値の線形性を利用して
\( E[g(X)] \approx E[g(\mu)] + g'(\mu) E[(x – \mu)] + \frac{1}{2} g”(\mu) E[(x – \mu)^2] \)
ここで期待値の性質から定数はそのままになり \( X \) の期待値は \( \mu \) なので
\( E[g(\mu)] = g(\mu), \, E[(x – \mu)] = 0 \)
よって
\( E[g(X)] \approx g(\mu) + \frac{1}{2} g”(\mu) V(X) \)
と近似できます。
同様に、これを利用して分散の場合は二次まで近似して
\( V(Y) = V(g(X)) \approx V(g(\mu)) + V\{(X – \mu) g'(\mu)\} = V(g(\mu)) + \{g'(\mu)\}^2 V(X) – \{g'(\mu)\}^2 V(\mu) \)
ここで定数の分散は0であることから \( V(g(\mu)) = 0, \, V(\mu) = 0 \) なので
\( V(Y) \approx \{g'(\mu)\}^2 V(X) \) と近似できます。












コメントを残す