因果推論の用語を整理する② -識別性の条件-

前回の記事では因果推論の基本となる潜在的結果(potential outcome)から個体因果効果(ICE)、平均因果効果(ACE)の定義、これら因果推論の前提となるSUTVAについて勉強してみました。

今回の記事では平均因果効果を推定するために必要となる識別性(identifiability)について勉強してみたいと思います。用語が多くて混乱するのですが、疫学(epidemiology)では識別性と関連した意味を交換可能性(exchangeability), 一致性(consistency), 正値性(positivity)といった単語で表現していることがあります。これらとの関連も一緒にまとめてみようと思います。

識別性(identifiability)の条件

平均因果効果を知りたいというケースは多いです。例えばある母集団に対して治療の有効性を検討しようとした場合、平均因果効果が分かれば、どのくらい治療によって差が生まれるのかが分かります。

そこで、どのような条件が揃っていれば平均因果効果を推定できるのか、という条件を示したのが、これから書いていく識別性の条件です。*1,2

条件は二つで、正値性(positivity)と独立性と言われています。順番に見ていきます。

正値性

正値性は簡単に言えば、介入をされる確率、介入をされない確率がいずれも0にならないようにする条件です。単純に考えて、標本の中で介入をされる人が0、あるいは介入をされなかった人が0であれば、単群の試験となってしまい、どうしたって平均因果効果は推定できないであろうことはイメージできますね。

具体的な数式として前回記事と同様に、介入の変数をT(介入ありがT=1、介入なしがT=0)として考えてみましょう。そうすると正値性というのは以下の式で表現することができます。

\(0\lt P(T=1)\lt1\)

介入群に割り付けられる確率が0より大きく1より小さい、というわけです。介入群に割り付けられる確率が0となってしまえば、前述したように因果効果の推定はできません。また、介入群に割り付けられる確率が1となってしまうと介入なしの対照群に割り付けられる確率が0になってしまうのでこれまた因果効果の推定ができなくなります。

いずれも0にならないようにするのがこの正値性という条件になります。

独立性

もう少し難しいのがこちらの独立性です。これは介入の割り付けと潜在的結果が独立である、という条件になります。まず具体的な例を二つほど考えてみます。

独立性の具体例

感染症による死亡の有無(結果）とその治療薬の有無(介入）の関係を見た観察研究を考えてみます。

この感染症では
①重症であると薬が投与されやすいが、死亡率が高く
②軽症であれば薬があまり投与されないが、死亡率は低い
としてみましょう。

そうすると感染症による死亡(結果）、治療薬(介入）、重症度の関係を見たとき、介入あり・なしで分けてみると以下のよう状況になります。

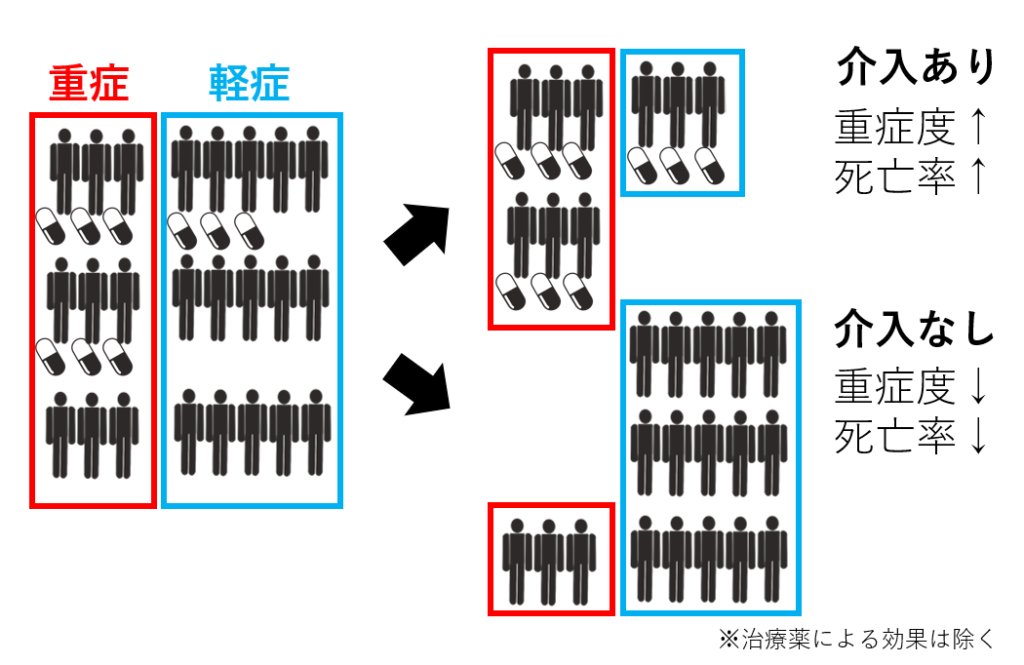
薬による治療の効果を抜いて考えた場合、介入ありの群では、重症が多いことから全体に死亡率が高く、介入なしの群では、軽症が多いことから全体に死亡率が低いわけです。つまり、治療薬(介入）の割り付け＜※治療薬の効果ではない＞と死亡(結果）は相関があり、独立ではありません。独立性を満たさないため、そのままだと平均因果効果の推定はできないということになります。

では、独立性を満たすのはどのような場合でしょう。

一つはランダム化比較試験の場合です。先ほどの例であれば、治療薬の有無を重症度と関係なくランダムに割り付けてしまえば、重症度は各群で均一になります。

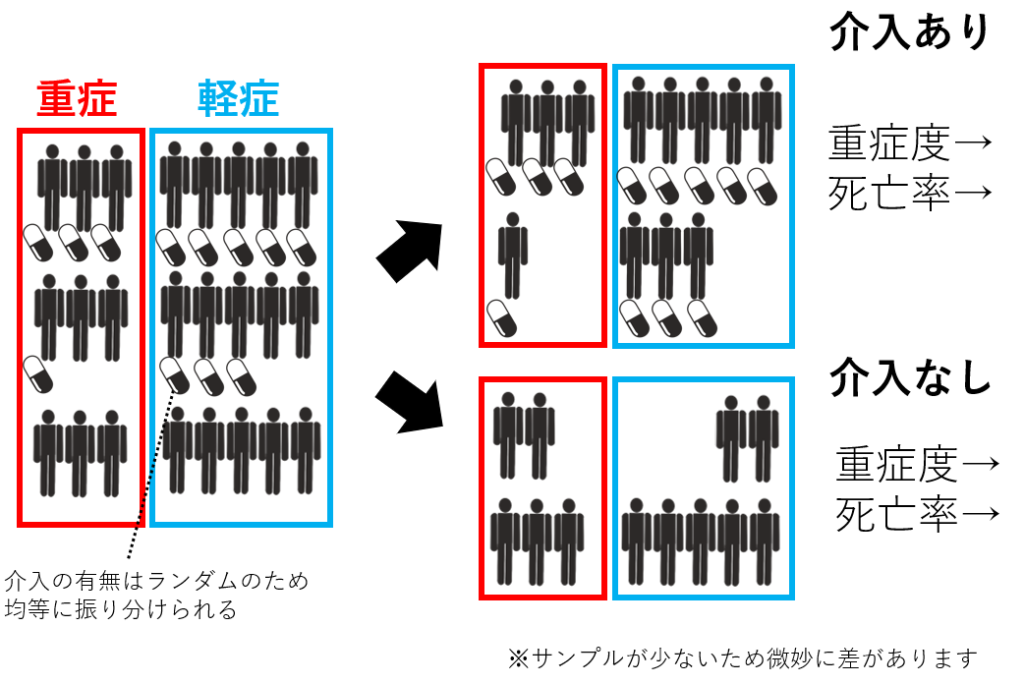
こうすれば独立性と正値性の条件を満たすため、平均因果効果の推定が可能です。

独立性の数式

では、続いて独立性がなぜ推定に必要であるのかを、数式で考えてみようと思います。

ここからは
死亡の有無をY(死亡がY=1、生存がY=0)
介入の有無をT(介入ありがT=1、介入なしがT=0)
重症度はX(重症がX=1、軽症がX=0)
とします。

また前回記事と同様の記載方法でY(0)がT=0(介入なし）の場合の潜在的結果変数、Y(1)がT=1(介入あり)の場合の潜在的結果変数としましょう。まず、求めたい平均因果効果の式は以下のようでした。

\(ATE=E[Y(1)]-E[Y(0)]\)

ところがこの潜在的結果変数Y(1),Y(0)は各個体に対して常に片方しか観測できません。実際に観測できるのは潜在的ではない結果変数Yを介入の有無で条件付けしたE[Y|T=1]とE[Y|T=0]です。ここからどのようにして、平均因果効果を求めるかが問題です。

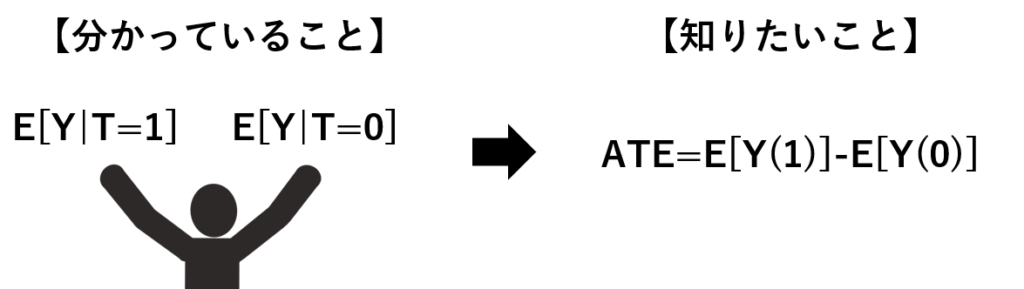
このとき必要になるのが独立性の条件です。独立性を数式で書くと以下のように表現されます。

\(\{Y(0),Y(1)\}\bot T\)

ここで、潜在的結果変数Y(0),Y(1)と介入の割り付けを表すTが独立であれば、条件付き期待値と条件付きでない期待値が一致することを利用します。

そもそも条件付き期待値の定義は

\(E[Y|X]=\sum yP(Y|X)\)(離散型）
\(E[Y|X]=\int yf_{Y|X}(y|x)dy\)(連続型）

でした。

ここで、XとYが独立であれば

\(P(Y|X)=P(Y), f_{Y|X}(y|x)=f_Y(y)\)

となりますので、離散・連続いずれの場合もE[Y|X]=E[Y]が導けます。
つまり、Tと潜在的結果変数が独立であれば条件付けしようがしまいが関係ないわけです。

よって

\(E[Y(1)]=E[Y(1)|T=1]\)

となります。さらに、ここで介入ありの潜在的結果の期待値(E[Y(1)|T=1])と現実での結果の期待値(E[Y|T=1]）は基本的に一致します。潜在的結果が現実になっただけなので当然といえば当然ですね（細かい話を言えば後述のSUTVAの第2条件≒consistencyが必要になります）。

よって

\(E[Y(1)]=E[Y(1)|T=1]=E[Y|T=1]\)

となります。さて、こうなると平均因果効果の式が現実に求められるものになったことが分かります。T=0の場合も同様に考えると平均因果効果は

\(ATE=E[Y(1)]-E[Y(0)]\\=E[Y|T=1]-E[Y|T=0]\)

と変形することができ、実際のデータから無事推定することができるのでした。ちなみに、正値性がないとE[Y|T=1]もしくはE[Y|T=0]が計算できないので、正値性も前述した通り必要となっています。

実は上記まで厳しい独立性の条件でなくても、平均因果効果は理論上推定できます。この辺りの話はexchangeabilityの分類とも絡むので後述します。

条件付き独立性

ここまででランダム化比較試験では独立性が担保され、平均因果効果が導き出せることは分かるのですが、それだけで終わってしまったら何の意味もありません。

そこで出てくるのが条件付き独立(conditionally independent)という用語です。識別性の条件を満たせば平均因果効果が推測できるわけなので、ある共変量で背景因子の調整を行う(条件付け)ことで独立性が担保できれば、理論上はランダム化比較試験と同様に平均因果効果が推定できるわけです。

例えば、前述の感染症の例でいけば重症度で条件付けを行う必要があります。まず、重症度で条件付けしなかった場合をみてみます。

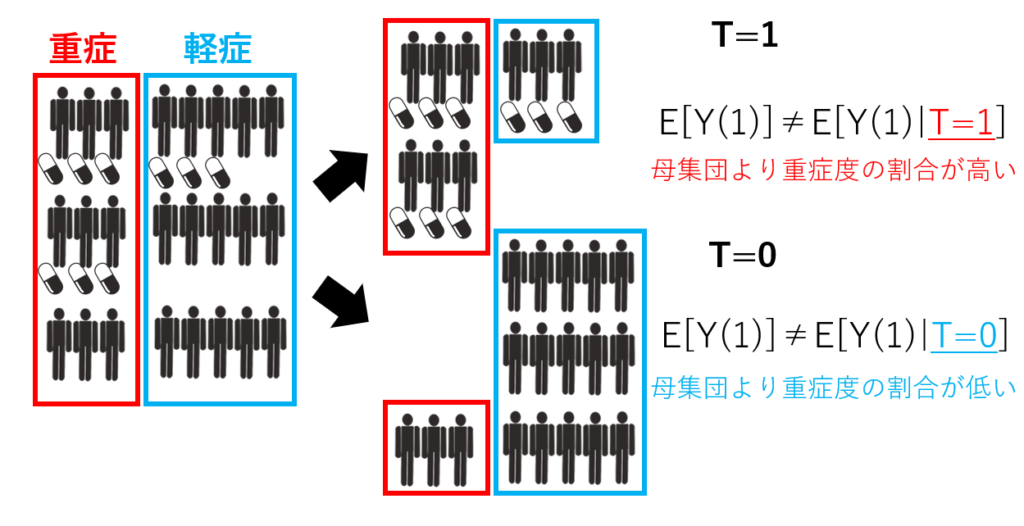
そのままだと介入群と対照群あるいは母集団でそれぞれ潜在的結果変数の期待値が変わってしまい、独立性の条件を満たさないため平均因果効果の推測は困難です。

そこで、重症度を新たな変数として加えて条件付けします。重症をX=1、軽症をX=0として層別化してみましょう。

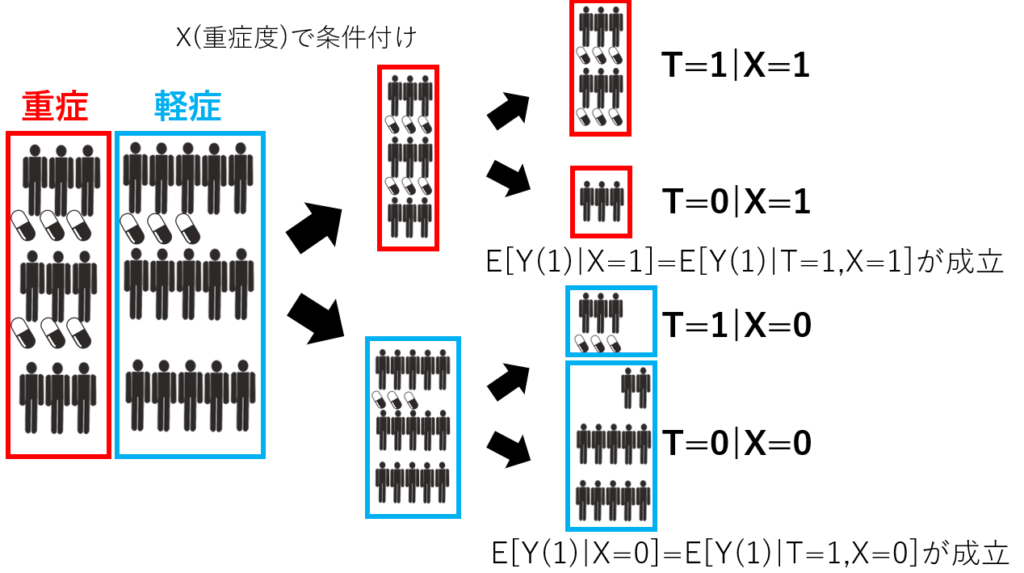
すると、条件付けの下では介入の割付と潜在的結果が独立となります。これを条件付き独立と言い、正値性と合わせて条件を満たせば、無事平均因果効果が推定できるわけです。数式として書くと先ほどの独立性の式に共変量Xを加えたものになります。

\(\{Y(0),Y(1)\}\bot T|X\)

難しいのは、実際多くの場合、共変量がここまで単純な構造ではないことです。今回は説明のため非常に簡素な例を想定しましたが、普通は背景因子がもっと入り組んでおり何をどのように共変量で条件付けするのかが問題となります。具体的な方法論として傾向スコア、操作変数法、逆確率重み付け法といった手法はいずれもこの因果推論の発想をもとに展開されていっているものだと思います。

また「共変量をどのように使うか」以前の問題としてそもそもどれで条件付けして、どれを条件付けしないのかということも実際困る点です。そこでどの背景因子を用いるべきかうまく整理するためのツールの例がDAG(Directed Acyclic Graph)です。因果推論の大家Judea Pearlが推奨している方法論で、こちらの著作などを参考にされるのが良いかと思います。

『入門統計学的因果推論』

リンク

当ブログでもDAGに関連した部分は一部紹介しております。

Judea Pearlの入門統計学的因果推論を読んでみよう① DAGとは？

さて、共変量を用いていかに因果効果を推測していくか、ここからが因果推論の本領発揮という部分だと思いますが、そこまで解説するような力量も経験もございませんので、ひとまずはこの混乱しがちな入門段階までで本記事を終えようと思います。

続いてもう一つ、よく出てくるためにさらに混乱を生みがちな疫学で使われる因果推論の用語についてみていきます。

疫学における識別性の条件

文献の引用元をみるにハーバード大学の疫学・生物統計の教授Miguel Hernánが提唱している用語であるようなので、その著作『what if』*3を参考にしながら用語の定義と前述の条件との関連性をみていきます。

観察研究を条件付きでランダム化比較試験のように扱う方法として必要な条件を以下の3つにまとめています。

①exchangeability（交換可能性）
②consistency(一致性）
③positivity(正値性）

ここまでに紹介してきた統計学における用語との関連性としては概ね(微妙な違いはありますが）以下のような関係性になっています*2。

exchangeability → 独立性
consistency → SUTVAの第2仮定(No Hidden Variations of Treatments)
positivity → positivity(変わらず）

ではもう少し詳しくみていきます。

exchangeability(交換可能性）

exchangeabilityの定義としては、ここまでの記事と同様の変数で説明しますと

\(P(Y(1)=1|T=1)=P(Y(1)=1|T=0)\)
\(P(Y(0)=1|T=1)=P(Y(0)=1|T=0)\)

とされています*3。これは何を言っているかといえば、1つ目の式は介入あり群も介入なし群も、もし仮に介入をした(潜在的結果）とするならば同じ確率で同じ結果が得られるよ、ということを表しています。

2つ目の式はもし仮に介入をしなかったならば、その場合もどちらの群でも同じ確率で同じ結果が得られるよ、ということになります。

具体的な方が分かりやすいので、感染症の例をもう一度考えてみると、ランダム化比較試験で介入ありなしを決めた場合は、もし仮に介入なしの群を全て急遽介入ありに変えたとしても、同じ確率で同じ結果が得られると考えられるでしょう。

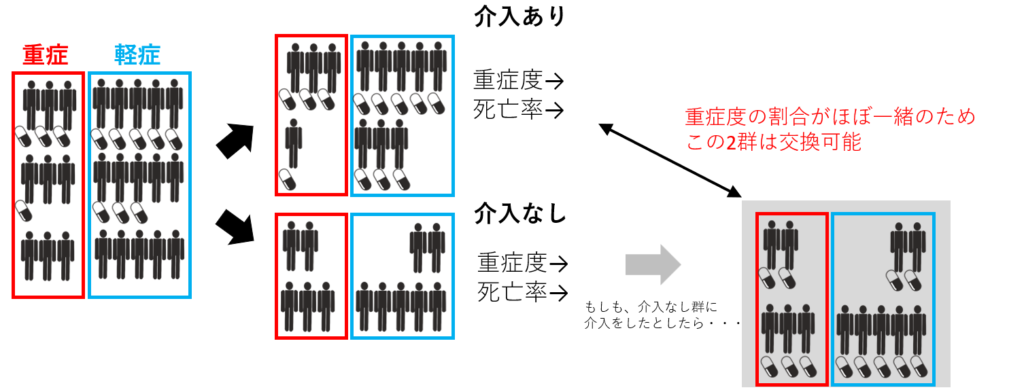
逆もまた然りで、介入あり群を急遽介入なしに変えたとしても同じ確率で同じ結果が得られることが推測されます。つまりexchangeabilityが成立するわけです。

これは介入の割り付けが潜在的結果と独立だからこそできることであって、独立性と同じ条件であることが分かります。

独立性が担保されていない状況も考えてみます。ランダム化割り付けではなく、介入の頻度が重症度によって影響を受けるとした場合に、介入なし群を急遽介入ありに無理やり変えてみたと想定したらどうでしょうか。

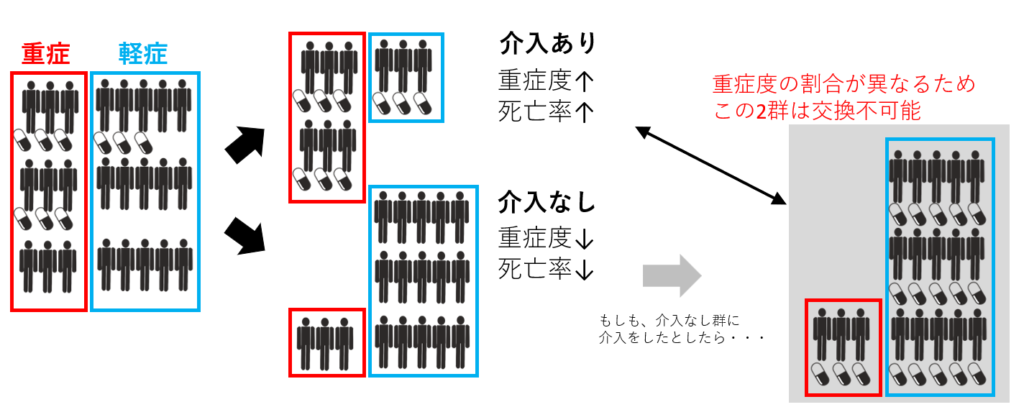
軽症が多い分、もともとの介入あり群と比べると結果は明らかに良くなることが推測されます。つまり、exchangeabilityが成り立たないわけです。

さて、ここまでで交換可能性の意味と独立性との類似性をある程度まとめられたと思いますが、交換可能性の中にはさらにfull exchangeability, mean exchangeabilityという分類があるのでそこを少し掘り下げます。

ここで先ほどの「独立性まで厳しくなくても実は平均因果効果を推定できる」という話に戻ります。

式変形の過程をみるとわかるように平均因果効果を推定するためにはこの等式が成り立てば良いわけです。

\(E[Y(1)]=E[Y(1)|T=1]\)

なので、確率あるいは確率分布の等式が成り立たなくても期待値さえ一緒であれば別に推定に問題はありません。期待値においてこの等式が成り立つことをmean exchangeabilityと呼んでいます。先ほどの例のように、全てのパターンの介入による潜在的結果変数(ここまではT=0,1としていましたが、複数の介入がある場合もある)の確率に関して交換可能性が成り立っている場合をfull exchangeabilityと言うようです。

mean exchangeabilityが成り立てば平均因果効果の推定はでき、full exchangeabilityまでは必要ないと言えます。

個人的にはmean exchangeabilityは成り立つけれどfull exchangeabilityは成り立たないとかそういう状況が実際に起こり得るのかどうかがよく分かりません。分布はよくわからんけど期待値だけは交換可能だよ、って状況があるのでしょうか。因果推論におけるメジャーな和書である『統計解析スタンダード統計的因果推論』*2を見ても「実際上は独立性を要請することが多い(p.84)」とあります。何か事例があれば教えていただきたいところです。

consistency(一致性）

consistencyの定義は介入が同じであれば、潜在的結果と現実の結果が一致しなければいけないというものです。

これまでの例と同様に介入をT=0,1で表現して数式で表してみます。T=1のときに実際に結果Yが得られたとします。そうすると

\(Y(1)=Y\)

が成立しなければいけません。これがconsistencyです。
当然のように思えますが、この等式が成立するにはSUTVAの第2仮定である”No Hidden Variations of Treatments”が成り立たなければいけません。T=1で介入ありとされるものの中で、実はいくつか違うパターンが内包されているとすると、この等式が成り立たなくなるかもしれないわけです。

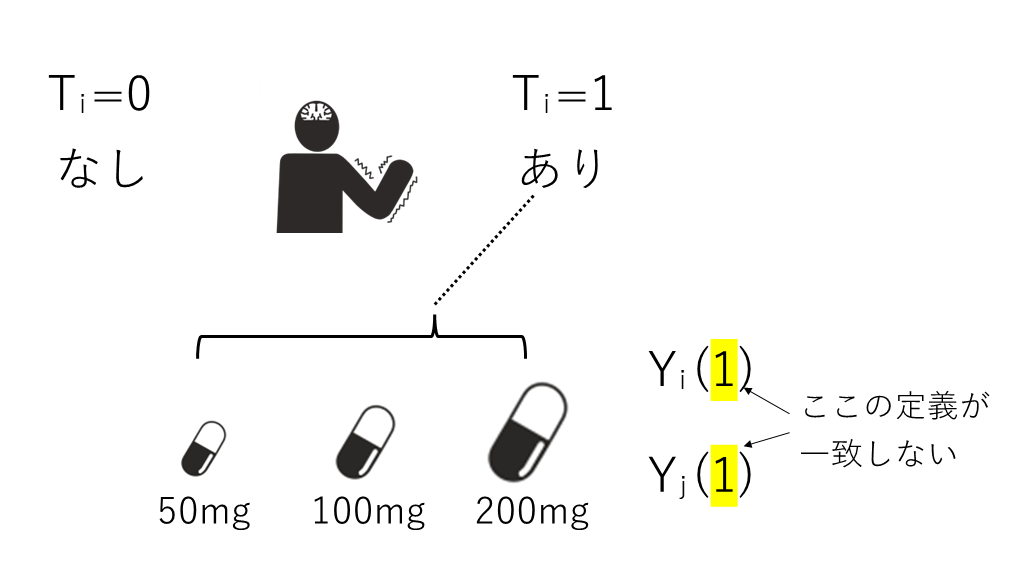
この前提は独立性の説明でも実は必要となっています。

\(E[Y(1)]=E[Y(1)|T=1]=E[Y|T=1]\)

この等式の最後の部分はconsistencyがなければ成立しません。多数の個体を対象とする平均因果効果の推定にはそもそもSUTVAが必要であることは前回の記事でも述べたとおりで、それが前提となっています。

positivity(正値性）

正値性は上記で説明したものと同様かと思いますので、意味については割愛します。

ランダム化比較試験なんかを想像するとこんなの当然成り立つでしょ、と思うわけですが、観察研究において条件付き独立性を考えたりするときには注意が必要なことがあります。

共変量が1つや2つだったら良いかもしれませんが、共変量の数が増えてきたときに介入あり、なしのどちらかのデータが欠けることがあり得ます。

例えば、女性で、アジア人で、体重60kg以上で、もともと抗凝固薬を内服していて、脳梗塞の既往があって、認知機能が正常で、普段から運動習慣があって、ADLが自立している人、といった沢山の共変量で条件付けしたときに介入ありの人はいても、介入なしの人はいない、、、なんてことも起こり得るわけです。

解析の内容によっては注意が必要と思われます。

まとめ

・識別性の条件は正値性(positivity)と独立性から成る。

・正値性は全ての介入に対して、それぞれをとる確率が0にならないようにすること。

・独立性は介入の割り付けと潜在的結果が独立であること。

・適切に行われたランダム化比較試験はこれらの条件を満たす。観察研究では条件付けをしてこれらの条件を満たすようにする必要がある。

・疫学において識別性の条件とされるのはexchangeability, consistency, positivityの3つ

・exchangeabilityは独立性の条件と類似している

・consistencyはSUTVAの第2仮定に近い