傾向スコアなどの勉強をしていく過程で、因果推論(causal inference)に関連した本をいくつか読んでいますが、因果推論という分野がそれを確立するための独特な用語が多いんですね。
こうした本を読み進める上で何度も用語が登場するのですが、どうも慣れていないと「この単語ってどういう意味だっけ?」とか「これを推定するにはどういう条件がいるんだっけ?」と混乱してしまいます。大抵は本の序章に書かれている内容なんですが、なかなかその概要をつかむのが難しいと思いました。
というわけで、因果推論の基礎となる単語を図を多用しつつ一度まとめてみたいと思います。例によってどこぞの大学等で教えられているわけでもないので、誤りがあったらご指摘いただけますと幸いです。可能な限りメジャーな文献、元文献を参考にしつつ書いてみます。
因果推論(causal inference)と潜在的結果(potential outcome)
まずそもそも因果推論とは何なのか。
因果推論は原因と結果の関係を考えるための方法論で、ある結果に対して原因とその影響の程度をどのように推測するかを示したものです。
その前に因果はどう定義すべきか、という話になりますとかなり混み入った話となり、哲学的で結論が出ない話となってしまいます。この辺りは『科学哲学からのメッセージ』*1が詳しいですが、そこはひとまず置いておきましょう。
因果の定義として最も良いのかどうかはともかくとして、現在進められている因果推論は役に立つ方法論として提案されています。「もしこの介入(原因)をしたらどうなる(結果)のだろう」という需要の大きい疑問に応えるものだからです。
例えば医学において患者さんに対する治療を行ったときにいつも医師が悩むのは「何故こうなったのか」あるいは「どうしたらこうならずに済んだのか」といったことです。ある人に手術をしたことで合併症で亡くなったしまった場合は、手術をしなければ良かったのではないか、と考えることもありますし、ある人に薬を処方して良くなったときには、薬が効いたのだ、と考えて、処方しなかったら良くならなかっただろう、と考えたりします。
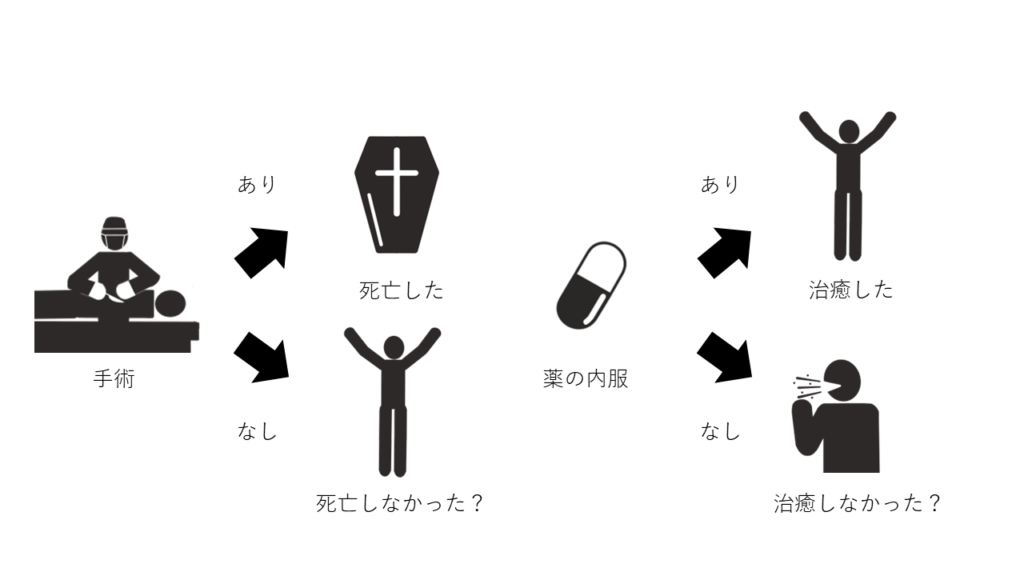
注目すべきはここで暗に「実際にやらなかったこと」を想定していることです。最初の例で「手術をしなかったら患者さんが亡くなることはなかったのではないか」と考えていますが、本当は分かりません。しなくてもその病気の影響で亡くなっていたかもしれませんし、別の原因で亡くなったかもしれません。もう一つの例として「薬を処方しなかったら良くならなかっただろう」というのも、本当は分かりません。病気が自然に改善したかもしれないからです。
これを想定していないのがいわゆる3た論法です。使った、治った、だから効いた、という誤った論法ですが、ここで問題なのは「使ったから治った」のかどうかは本当は分からないということです。これをきちんと「手術が原因で死亡という結果となったのか」「薬が原因で治癒という結果となったのか」を検討する方法論が因果推論というわけです。
現実では、実際に起きなかった結果を知るための方法論は因果推論ですが、想像の世界ではそれ以外の方法がよく出てきます。例えばタイムリープ、タイムマシン、未来視といった類のものです。ある介入(原因)を行ったときに、未来ではどうなっているのか(結果)、それを確認した上で介入を変えて、未来が再度変わるかを確認する、というのは良くある流れですね。これをイメージすると話が少し分かりやすい気がします。
例がありすぎて困りますが、映画だと『バタフライ・エフェクト』『バック・トゥ・ザ・フューチャー』『ターミネーター』『ミッション:8ミニッツ』とかですね。因果推論の大家であるRubinは『素晴らしき哉、人生!』という映画を挙げています*2。これは仮に主人公が存在しなかった世界がどうであったかを天使によって見せられるというエピソードとなっています。
アニメ・漫画だと『東京卍リベンジャーズ』『僕だけがいない街』『STEINS;GATE』『時をかける少女』『All you need is kill』などなどこちらも枚挙にいとまがありません。いずれの話も自身が行った介入とその結果を何度も確認しながら話が進んでいきます。漫画でよくある未来視の能力者というのもこれに近いものがあって①何もしなかった場合の結果をみて自分の行動を変えて②行動を変えた結果を経験するということで、介入(行動を変える)ありなしでの結果を見ています。最近の漫画だと『チェンソーマン』のアキの能力とかですかね。未来視の能力者にありがちなことですが、介入によって変わらないこともあるわけです。
これらの例はいずれも何か行動を変えることで結果がどう変わるのかを考えています。因果推論の考え方も基本的にはこの思考に則っています。先程も紹介しました因果推論の大家であるRubinは著書の冒頭で“no causation without manipulation”という言葉を使っています。何らかの介入がなければ因果を想定できないわけです。どんな介入に対してどんな結果を考えていくかを明確にすることが因果推論では必要となってきます。
なお、この介入というのがどこまでの行為を指すのか(例えば、内服の有無などは分かり易いのですが、性別・人種といった属性の違いはどう扱うべきなのか)は意見が分かれるところでもあるようです*3。今回は用語の整理が目的なので単純な例を扱うこととしていきます。
ここで、介入と結果を考えるときには、上記の例で述べてきたように必然的に反事実モデル(counterfactual model)と呼ばれる「実際に介入をしなかったらどうなったのか」を考えないといけません。
そこで潜在的結果(potential outcome)を定義します。
潜在的結果とはある個体(医学分野ではほとんどの場合、ひとりの人)にある処置(医学分野では薬や手術などの治療法)を行った、あるいは行わなかったときに得られるであろう結果のことを指します。これを計算可能なように数学的な記号で整理していくわけです。
例えばある治療を行った場合をT=1, 治療を行わなかった場合をT=0とします。そして仮に治療を行ったら治癒したと考えられる場合はY=1, 治癒しなかったと考えられる場合はY=0と定義します。さらに個体を示すため、あるi番目の人の結果を添字として示してみます。
治療を行った場合にi番目の人が治癒する、というのは以下のように表されます。
\(Y_i(T_i=1)=1\)
式の書き方は書籍によってばらつきもありますが、T=1を1と省略して書くこととしますと
\(Y_i(1)=1\)
と書きます。治療をしなかった場合も治ったであろうという場合は以下のように書きます。
\(Y_i(0)=1\)
ある個体に対して治療をした場合としなかった場合は両立しませんので、この\(Y_i(0), Y_i(1)\)というのは「潜在的」結果変数と呼ばれます。現実にはこの二つの変数が両立しないことから現実の結果変数Yは以下の式で表現されます。
\(Y_i=(1-T_i)Y_i(0)+T_iY_i(1)\)
\(T_i=1\)であれば右辺の第1項が0となりますので
\(Y_i=Y_i(1)\)
となりますし、\(T_i=0\)であれば右辺の第2項が0となりますので
\(Y_i=Y_i(0)\)
となります。現実にはどちらかしか分からないことが式で表現されているわけです。
式のイメージを膨らませるためにもう少し卑近な例で考えてみましょう。半分趣味なので、もう十分に分かったという方は読みとばしてもらって良いです(笑)。『ドラゴンボールZ』の人造人間編を考えてみます。
〜ドラゴンボールを知らない人のためのあらすじ〜
孫悟空(主人公)は強敵人造人間と戦うこととなったが、タイムマシンを使って未来から来た仲間であるトランクスから自分が心臓病で亡くなることを知らされる。トランクスは最も強い悟空を救うために心臓病の薬を未来から持ってくる。
トランクスが未来から持ってきた心臓病の薬を飲む(介入)ことで孫悟空(個体)は心臓病にならずに済む(潜在的結果)わけです。逆に、トランクスが未来から来なければ孫悟空は心臓病になり、亡くなってしまいます。
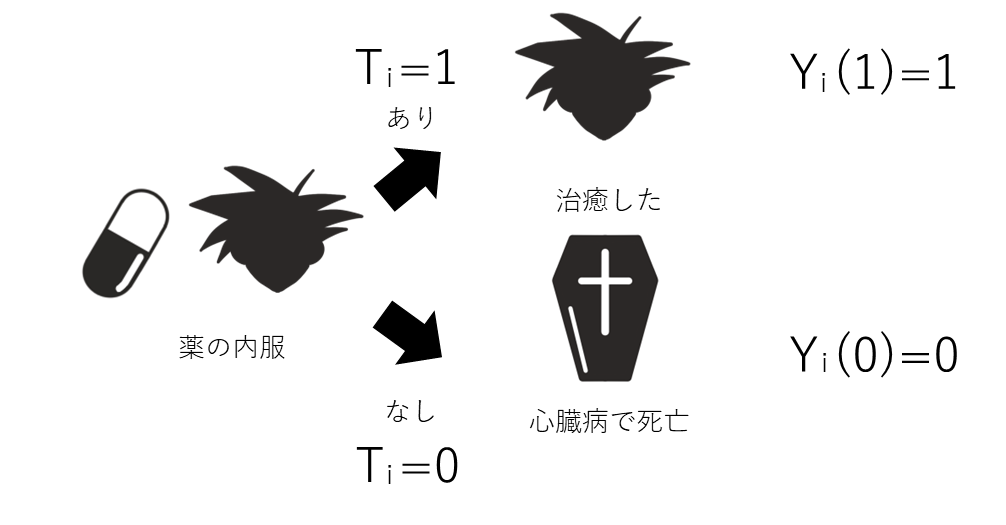
さてここで話を現実に戻しますと、現実世界ではタイムマシンはありませんので、この二つの潜在的結果のうち、ひとつしか観測できません。仲間である地球人の戦士クリリンからみたらどちらかの世界しか経験されないわけです。あくまで二つの結果というのは潜在的結果です。
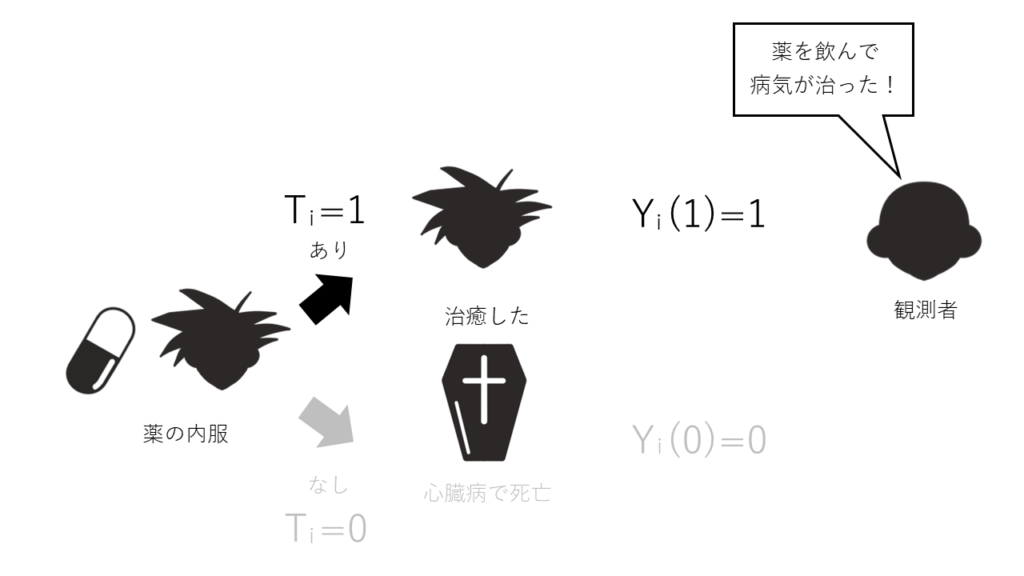
この観測できなかった値をほかの情報を用いて何とか推測していこうというのが因果推論の目的となっています。つまり、欠測したデータを推測するわけなので、因果推論はアウトカムの欠測データの問題と考えることもできます*4。アウトカムの欠測とはランダム化比較試験やその他のコホート研究でも起きうる現象で、転居、副作用による試験の脱落、試験参加の同意撤回、死亡など途中でフォローアップできなくなり、アウトカムが確認できない場合を指します。そうしたときに使われるのが統計的な手法による欠測データの補完です。その人と同様な条件において仮に結果が欠測しなかった場合に、どのようになるのかを他のデータから推測します。この考え方は因果推論と同様となるわけです。
ここまでが因果推論で追い求めることとなる潜在的結果の話でした。
個体因果効果(ICE; Individual Causal Effect), 個体処置効果(ITE; Individual Causal Effect)
続いて、個体因果効果(ICE; Individual Causal Effect)あるいは個体処置効果(ITE; Individual Causal Effect)と呼ばれる用語の説明です。
個体因果効果(ICE)とはi番目のある個体が介入をされた場合の結果と介入をされなかった場合の結果の差をとったものです。つまり式にすると
\(Y_i(1)-Y_i(0)\)
となります。ただし、現時点では個体因果効果は決して計算することができません。何故なら、潜在的結果の項目で述べたように、潜在的結果変数は介入あり、なしの場合の片方しか観測することができないからです。
多くの本でこの問題はHolland(Rubinと共同で統計的因果推論を作り上げたとされる)の論文を引用して因果推論の根本的問題(Fundamental Problem of Causal Inference)とされています*5,6。確かに個体因果効果としては推測しようがないのですが、Hollandの論文ではそれに対して科学的な解決方法(scientific solution)と統計的な解決方法(statistic solution)を提案しています。例えば、科学的解決方法としては均質であるような条件を仮定できるような状況を作り出し、結果を調べてみることが提案されています。そして統計的な方法としては(個体因果効果ではありませんが)次に説明する平均因果効果(ACE; Average Causal Effect)を用いるような方法が提案されます。
なお、因果推論に関する日本語の主要な参考書である『統計的因果推論の理論と実装』によりますと個体因果効果を推測しようという流れもあるようで、手法が洗練されてきますとまだまだこれから状況は変わってくるのかもしれません*7。
平均因果効果(ACE; Average Causal Effect), 平均処置効果(ATE; Average Causal Effect)
平均因果効果(ACE)あるいは平均処置効果(ATE; Average Causal Effect)とは「ある個体」ではなく「ある集団」に対して潜在的結果変数の差の期待値をとったものを指します。
式で示すと以下のようになります。
\(E[Y_i(1)-Y_i(0)]\)
また期待値の加法性を用いれば
\(E[Y_i(1)]-E[Y_i(0)]\)
と書くことができます。
個体については先ほど述べたように潜在的結果の差を計算することができませんが、集団については欠測データをうまく補うことができれば推測することが可能です。ただ、これはあくまで対象とする母集団に対しての数値ですので、個体に対する効果ではありません。
では、これが実際に推測できるのかどうか、ということが次に問題となります。例えば、ランダム化比較試験ではそれぞれの個体においては潜在的結果の片方が欠測しているものの、ランダムで割り振ることによって全く同様の条件である個体が存在すると仮定できるため、理想的なランダム化比較試験であればこの推測はできることが分かります。
推測するためにどのような条件を満たすべきなのか、は識別性(identifiability)の条件としてまとめられていますが、また少し長くなるので、次回の記事で説明する予定です。
ここで最後にもう一つ、解析の対象を個体ではなく集団に広げる際に因果推論を行う前提条件として必要となるSUTVAについて説明してみます。
SUTVA(Suitable Unit Treatment Value Assumption)
SUTVA(Suitable Unit Treatment Value Assumption)とは複数の個体に対して因果効果を推定する際に必要となる仮定のことを指します。和訳がどうにもしにくい言葉であるため、そのまま使われることが多いです。英語のぱっと見からは意味が掴み辛いのですが、大事な前提であるためよく知っておかなければいけない用語です。これは大きく2つの条件から成っています。
- No Interference
- No Hidden Variations of Treatments
具体例を交えながらそれぞれ見ていきます。
1. No Interference
“interference”とは干渉を意味する言葉で、対象となる集団内の個体がそれぞれ干渉し合わないことが、因果効果の推測において必要であることを示しています。
どういうことかと言いますと、その研究で必要となる介入によってはある個体に対する介入が周囲の個体のアウトカムに影響を与えることがあります。例えば、ワクチンの接種(介入)がある感染症の発症(結果)に与える因果効果を推測しようとしたとします*8。i番目の個体(iさん)、j番目の個体(jさん)、k番目の個体(kさん)をそれぞれ考えた時、この3人が一緒に暮らしていたとしたらどうでしょう。ワクチンに効果が多少なりともあると仮定した場合、jさんにワクチンを打つと、一緒に生活するiさん、kさんはワクチンを打つにせよ打たないにせよ、感染症にかかりにくくなり、結果に影響が出るのではないでしょうか。
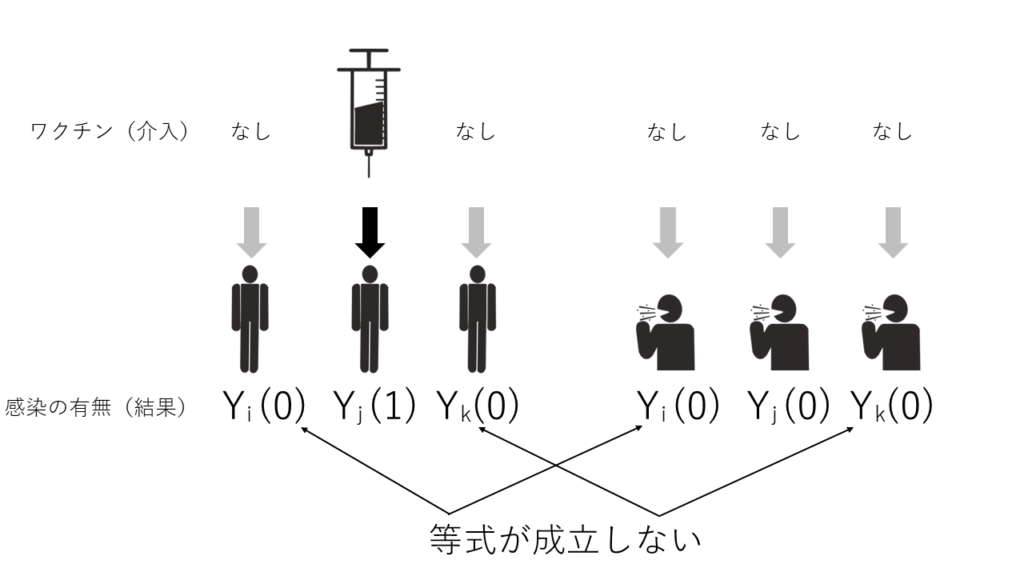
つまり、因果推論の式で表現した場合
\(Y_j(1)のときのY_i(0),Y_j(0)\)
と
\(Y_j(0)のときのY_i(0),Y_j(0)\)
は異なるものとなってしまいますね。
これでは同じ式が一致しないこととなってしまう(\(Y_i(0)\neq Y_i(0)\))ので、前提として問題が生じてしまいます。
こうならないためには、jさんの介入の有無とiさん,kさんの介入の有無を全ての組み合わせについて分けて結果変数を定義する必要があります。例えば、
\(Y_{i,j,k}(0,1,0), Y_{i,j,k}(0,0,0,)\)
という感じですね。こうなると全ての組み合わせについて結果変数が定義され、そこからの平均因果効果の計算は困難を極めます。なので、前提としては干渉し合わないこと、がまず必要となるわけです。
他の例としてRubinは教育プログラム(介入)によって収入(結果)が受ける因果効果をあげています。
iさん、jさん、kさんを考えた時に、jさんのみが教育プログラムを受けたとしましょう。そうすると効果があると仮定した場合にjさんのみが優秀な教育成果を得られるので、jさんは良い収入を得られるだろうと予想されます。
ところがiさん、jさん、kさんのみんな(あるいはもっと大きな集団全体が)教育プログラムを受けたとすると、どうなるでしょう。集団全体が大規模に同じ成果を得られたとしたら、経済の詳しいことは分かりませんが、おそらくは最初の例と同様には収入が上がらないのではないでしょうか。一人が差別化されていれば、その人が良い職を得られるのかもしれませんが、皆同様となったらそういうわけにはいきません。
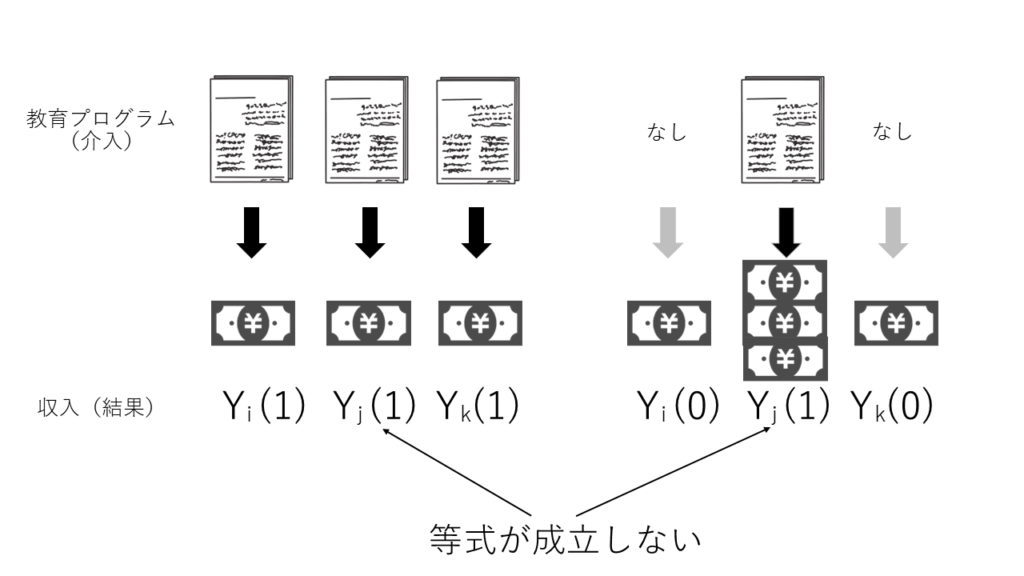
これもinterferenceを示す一例となっています。
2. No Hidden Variations of Treatments
さて、もう一つの条件は介入の内容が数値で定義されたものと実は異なるということがあってはいけない、ということを示しています。これも先ほどと同様に、複数の対象を考えた際の潜在的結果変数の定義に関わってくる問題です。
例えば、アスピリンの内服(介入)によって脳梗塞の再発(結果)が受ける因果効果を調べようとしたとしましょう。
介入は薬の内服あり、なしで定義されていますが、実際には研究を行う施設ごとに用量が違った(例えば50mg,100mg,200mg)とします。そうなるとどうでしょう、同じ結果変数で定義されていても実は得られる結果変数が施設ごとに変わってしまうのではないでしょうか。
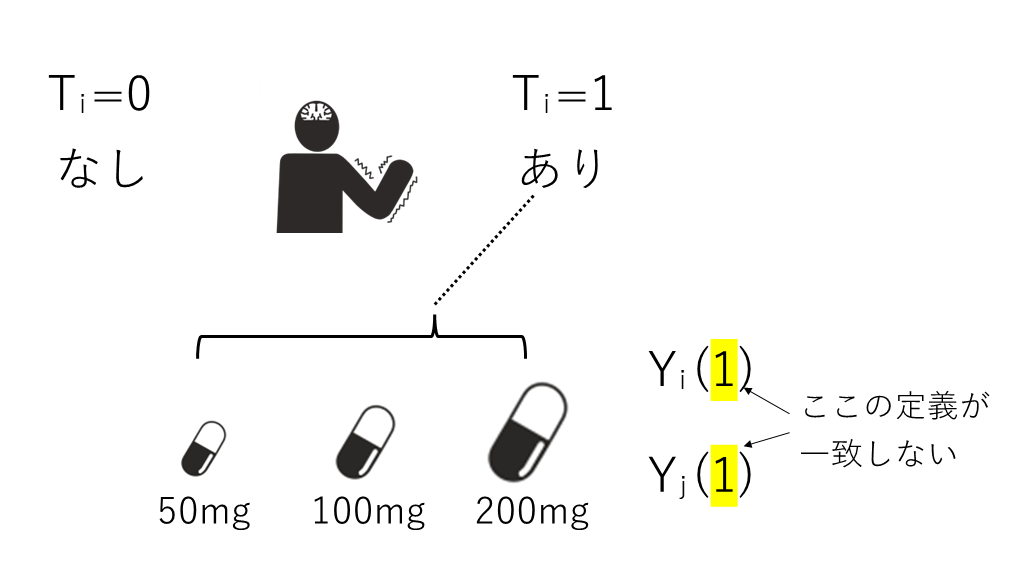
こちらも干渉の例と同様に同じ式であるはずのものが異なってしまう(\(Y_i(1)\neq Y_i(1)\))ので、因果推論を行う前提として誤っていることがわかります。
つまり、介入の方法はそれぞれの個体によって異なることがないよう統一されたものでないといけませんし、もちろん調べたい介入以外の方法で因果効果に影響を与える介入が含まれないようにしないといけません。
内容としてはNo Hidden Variations of Treatmentsではないように思いますが、Rubin本ではアウトカムの定義についても同様に各個体ごとで異なることがないようにしないといけないと指摘されています。
例えば、頭痛薬による介入で治療後に感じる頭痛の程度をアウトカムとしたときに、「変化なし」「軽度改善」「中等度改善」「頭痛なし」と4段階評価とすると軽度と中等度の違いといった細かな変化は、評価者によって基準が異なってしまう可能性があります。
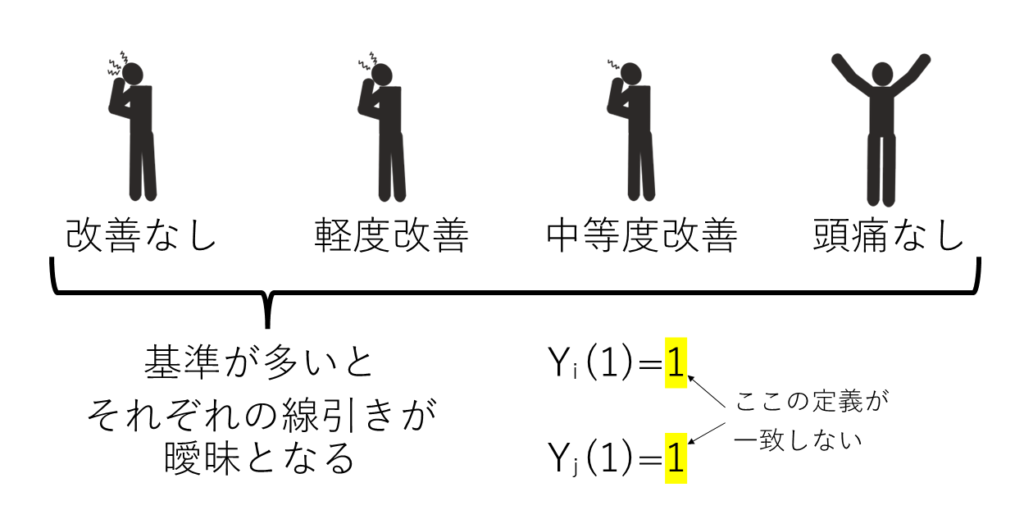
それに対してアウトカムを「頭痛あり」「頭痛なし」と粗い基準にしてしまえばこうした各個体ごとのアウトカムの違いは少なくなる可能性が高いです。
要するにSUTVAの二つ目の条件というのは各個体の潜在的結果と介入を十分に定義されたものにすることが大切ということですね。
また、このSUTVAについて因果推論の本でよく述べられているのは、本質的に除外的制約(exclusion restriction)である、ということです。これらの2つの仮定は求めたい介入以外のものによる因果効果を取り除くための制約であるというわけです。
ここで大事なことは、仮定を満たす条件を考えるためには、背景知識など解析対象となるデータの外部の知識を用いないといけないという点です。ここまでの例を振り返ってみてもわかります。今までの例がSUTVAを満たさない理由として
「ワクチンを投与すると周囲の人への感染が減る可能性がある」
「皆が同じ教育プログラムを受けるとおそらく収入は同じようなものとなる」
「アスピリンは用量によって効果が異なる」
「頭痛を軽度改善とするか中等度改善とするかは人によって判断が混在する」
といったものを挙げましたが、これはいずれも解析の対象となるデータから導き出すものではなく、事前に想定できる知識です。どの程度であればこれらの理由が問題となるかを外部知識によって判断しなければいけません(例えば、ワクチンが影響を及ぼす“周囲の人”とはどの辺りまで近い人を指すのか)。
因果推論を行うにはこうしたデータ外の外部知識も必ず用いないといけないことは同じく因果推論の大家であるJudea Pearlの本”The Book of Why”でも繰り返し強調されています*10。これだけ理論の大前提のとなる仮定で外部知識が必要となっていますので、データがあれば前提なしに問題の答えが出せる、というのは決して勘違いしてはいけない点だと思います。
まとめ
ここまでの用語の意味と関係性を簡単に整理してみます。
・潜在的結果はある個体が介入を受けた場合に取りうる結果のこと。現実には介入あるなしの片方の結果しか観測されない。
・個体因果効果は介入ありの潜在的結果と介入なしの潜在的結果の差。現実には計算できない。
・平均因果効果は集団に対しての介入ありの潜在的結果と介入なしの潜在的結果の差の期待値。識別性を満たせば推測できる。
・平均因果効果などでは対象が複数となるため、因果推論を行うためにはSUTVAという仮定が必要となる。
・SUTVAは1.No interference, 2.No Hidden Variations of Treatmentsという2つの条件から成る。対象となる個体間の相互干渉がないことと、介入(あるいはアウトカム)が個体間で変化しないように定義することが必要である。
次回の記事では平均因果効果の推測のために必要な識別性について、主に用いられる参考書を複数参考にしつつ、まとめてみたいと思います。因果推論の大前提となる用語の整理なので、次回でひとまず完結させる予定です。
参考文献・脚注
*1『科学哲学からのメッセージ』
因果の定義について歴史的な経緯と現在も続く様々な議論がまとめられています。因果推論も少し登場します。
*2『素晴らしき哉、人生(It’s a wonderful life)』
ウィル・スミスの映画とは別物です。こちらは観たことないのですが、ほかのタイムリープものの映画は結構どれもおすすめです。
*3 ここでいう介入は実際に行うことができなくても思考のうえで可能なことであれば良しとされているようですが、例えば性別などの属性についてはそれを変える介入とはどういうことか定義が難しいため、意見が分かれているようです。(『統計的因果推論の理論と実装』p.6参照)
*4 『Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction』
和書でもよく引用されているRubinの著作です。
*5, 6 『統計的因果推論の理論と実装』『統計解析スタンダード 統計的因果推論』などで取り上げられています。Hollandの元論文はこちら。1986年の論文で、実はこのあたりの話が出てきていたのは結構前であることがわかります。
Statistics and Causal Inference
*7 『統計的因果推論の理論と実装』p.295
個体因果効果が推測できたらまさに未来視に近いものなので実に興味深い話です。
*8 『Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction』ではワクチン、教育プログラムが例として出されています。こう考えるとワクチンの効果を推論するというのはかなり難しい要素を多数含んでいることがわかります。
*9 『The Book of Why』
因果推論の大家の一人でDAG(Directed Acyclic Graph)を推しているJudea Pearlの本です。もうちょっと一般向けの本かと思いきや、歴史も交えながら結構ガチな因果推論とDAGの理論を繰り広げる本でした。おススメです。














コメントを残す