サンプルサイズの計算方法として簡易的な方法とされるLehr’s formula。『統計検定1級対応 統計学』でも医薬生物分野の章で紹介されており、過去問では2018年の医薬生物学分野で出題されています。
そこで、この記事ではLehr’s formulaの式、導出方法と過去問での応用を見ていきたいと思います。導出に関しては帰無仮説、対立仮説や有意水準、検出力の応用として勉強になるので、ぜひ慣れておきたいところです。
早速見ていきましょう。
Lehr’s formulaとは?
サンプルサイズ計算を簡便に行うための式です。例えば、正規分布に従う独立な2群の平均の差を有意水準α、検出力1-βで仮説検定する場合に、予測される差δを設定すればサンプルサイズがどの程度必要なのかを計算することができます。
具体的な式を見ていきます。
確率変数\(X\sim N(\mu_X, \sigma^2)\)と\(Y\sim N(\mu_Y, \sigma^2)\)とし、検出したい差を\(\delta=\mu_X-\mu_Y\)とします。これを有意水準α、検出力1-βで両側検定したとすると、それぞれの群から必要なサンプルサイズをnは
\(n=2(Z_{1-\beta}+Z_{1-\frac{\alpha}{2}})^2×\frac{\sigma^2}{\delta^2}\)
となります。なお、\(Z_{\alpha}\)はそれぞれ標準正規分布における下側100α%分位点を指します。
また効果の差を標準偏差で割ったものをeffect size(ES)とすると先程の式は
\(n=\frac{2(Z_{1-\beta}+Z_{1-\frac{\alpha}{2}})^2}{ES^2}\)
となります。
さらにα=0.05, 1-β=0.8という慣例的に最もよく用いられる設定では概ね
\(n=16×\frac{\sigma^2}{\delta^2}\)
となります。非常に簡単な式なので、効果量と標準偏差から何となくサンプルサイズを想像する際には便利ですね。
なお、Lehr’s formulaについて調べた範囲で見つけられた元論文はおそらく1992年のこちらです。ここに先程の具体的な式と同じ式が載っています。
Sixteen S‐squared over D‐squared: A relation for crude sample size estimates – Lehr – 1992 – Statistics in Medicine – Wiley Online Library
Lehr’s formulaの証明
続いて証明を行なっていきます。
\(N(\mu_X, \sigma^2)\)に従う確率変数Xと\(N(\mu_Y, \sigma^2)\)に従う確率変数Yという独立した2群から同数n個を抽出した標本について考えます。
標本の平均と分散はそれぞれ
\(N(\mu_X, \frac{\sigma^2}{n})\)
\(N(\mu_Y, \frac{\sigma^2}{n})\)
となります。また二つの平均の差を\(\delta=\mu_X-\mu_Y\)とおきます。
これを有意水準α、検出力1-βで
帰無仮説は\(H_0:\mu_X=\mu_Y\)
対立仮説は\(H_1:\mu_X\neq\mu_Y\)
という仮説検定をしたいとします。
このとき、帰無仮説の下での平均値の差の分布は
\(N(0,\frac{2\sigma^2}{n})\)
対立仮説の下での平均値の差の分布は
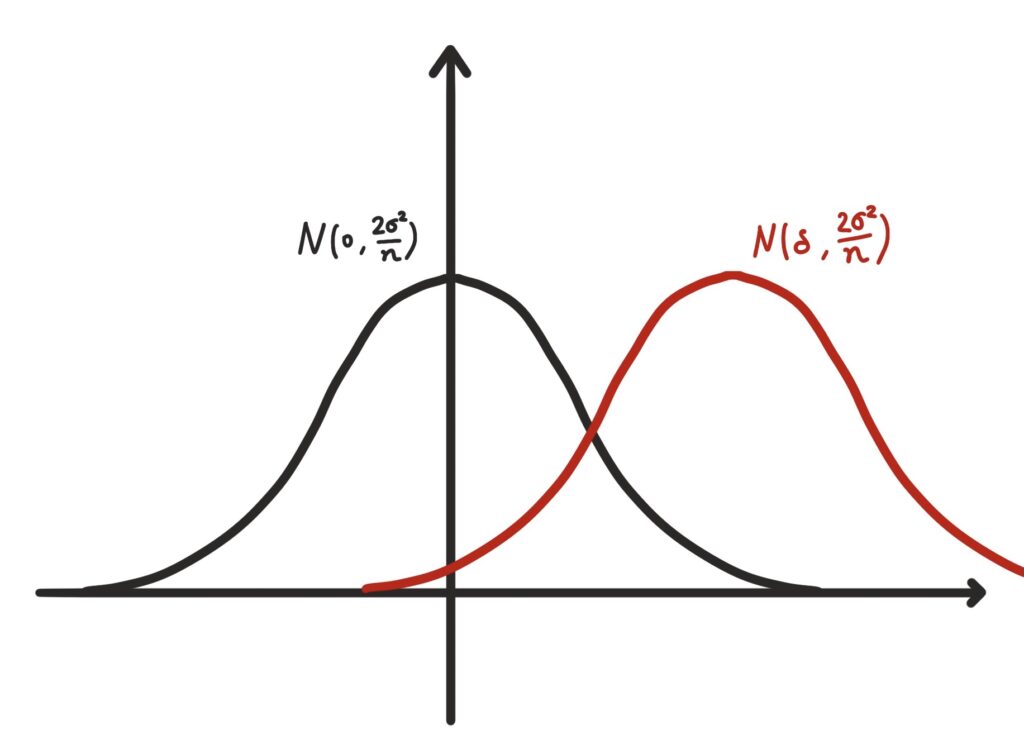
\(N(\delta, \frac{2\sigma^2}{n})\)
となります。グラフで表すとこんな感じですね。
さて、ここで帰無仮説における下側確率の分位点がどう表現されるか考えてみましょう。つまり、以下のグラフの星マークの部分を考えてみることになります。
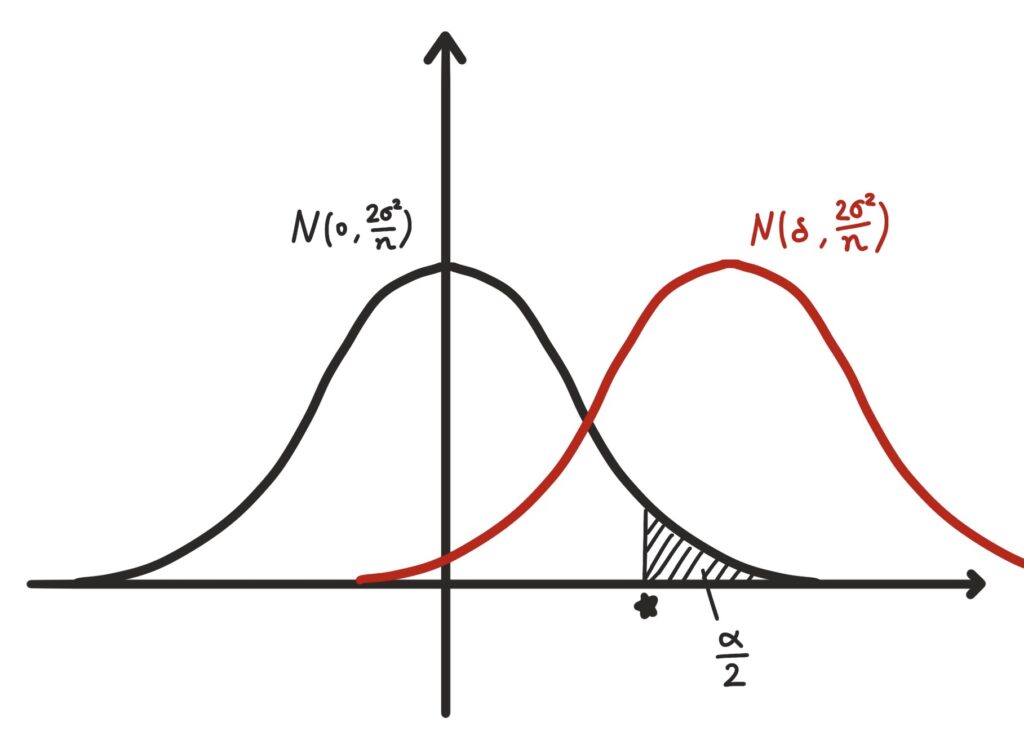
これは
\(Z_{1-\frac{\alpha}{2}}×\sqrt{\frac{2\sigma^2}{n}}\)
となります。
標準正規分布における分位点は、標準偏差が\(\sigma\)の正規分布に対しては、以下のように計算されます。
確率変数Xの上側100%分位点を\(x_\alpha\)とし、確率変数Yを\(Y=\sigma X+\mu\)と定義した場合、確率変数Yの上側100%分位点\(y_\alpha=\sigma X_\alpha+\mu\)となる。
これは『現代数理統計学の基礎』の練習問題に証明がありました。
続いて、グラフの星マークの部分を対立仮説の分布(赤)から考えてみます。
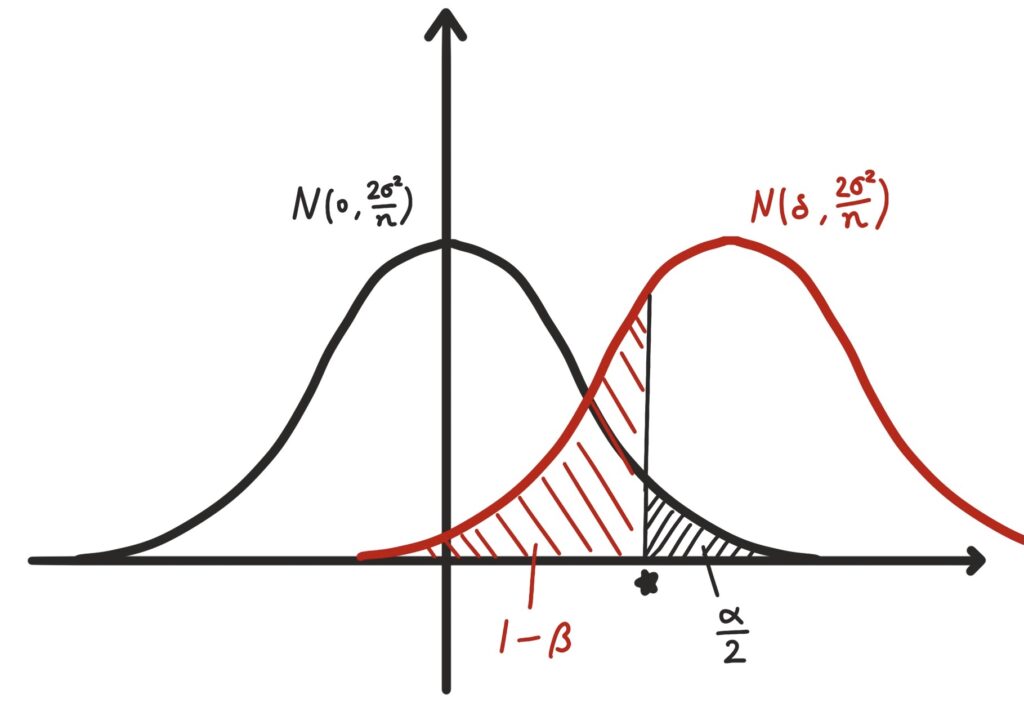
対立仮説の分布は平均がδですので星マークの部分は
\(\delta-Z_{1-\beta}×\sqrt{\frac{2\sigma^2}{n}}\)
となります。
帰無仮説の分布から求めた星マークの数値と対立仮説から求めた星マークの数値は一致するはずなので
\(Z_{1-\frac{\alpha}{2}}×\sqrt{\frac{2\sigma^2}{n}}= \delta-Z_{1-\beta}×\sqrt{\frac{2\sigma^2}{n}}\)
となります。
これを整理すると
\(n=2(Z_{1-\beta}+Z_{1-\frac{\alpha}{2}})^2×\frac{\sigma^2}{\delta^2}\)
となりますので無事証明できました。
統計検定1級における過去問の例
過去問では統計応用・医薬生物学分野で2018年問1(5)で出題されています。
問題としては、二つの群におけるハザードの差の対数が漸近的に正規分布に従うことを利用して求めるものでした。
この問題ではハザードの差の対数が対立仮説において漸近的に
\(N(log\lambda_1-log\lambda_2, \frac{2}{r})\)
に従い、帰無仮説においては
\(N(0,\frac{2}{r})\)
に従います。
よって先程の式と同様に考えると
\(Z_{\frac{\alpha}{2}}\sqrt{\frac{2}{r}}=(log\lambda_1-log\lambda_2)-Z_{\beta}\sqrt{\frac{2}{r}}\)
となるため
\(r=\frac{2(Z_\frac{\alpha}{2}+Z_{\beta})^2}{(log\lambda_1-log\lambda)^2}\)
となります。(この問題では上側100α%分位点を\(Z_\alpha\)としている点に注意)
参考:
http://www.columbia.edu/~cjd11/charles_dimaggio/DIRE/styled-4/code-12
















コメントを残す