(以下は上記動画のスクリプトを元に再構成したブログ版です)
今回紹介するのは「大人のための数学勉強法」。社会人になってから必要に迫られて数学を勉強しないといけなくなった、けれども数学はもともと苦手・・・。そんな人にはぜひ読んでほしい一冊となっています。
学生時代に「数学の問題集で答えを覚えてしまい、問題集は解けるけれども初見の問題は解けない、、、」という私のような経験がある人には役に立ちましたので、似たような経験がある人にはおすすめです。
目次の紹介
- はじめに
- なぜあなたは数学ができなかったのか?
- 数学ができるために必要な能力とは?
- この本の使い方。
- 第1部:数学はどのように勉強すべきか
- 暗記はしない
- 定理や公式の証明をする
- 「聞く→考える→教える」の3ステップ
- 自分の「数学ノート」を作る。
- 第2部:問題を解く前に知っておくべきこと
- 数学で文字を使うワケ
- 未知数は消去する
- 問題集の使い方
- 苦手な人に欠けている「解く」ための基本。
- 第3部:どんな問題にも通じる10のアプローチ
- 「次数を下げる」「周期性を見つける」「対称性を見つける」「逆を考える」「和よりも積を考える」「相対化する」「帰納的に思考実験する」「視覚化する」「同値変形を意識する」「ゴールからスタートをたどる」
- 第4部:総合問題10のアプローチを使ってみよう
- 総合問題の解説
まず目次から見ていきましょう。この本ではまず数学をどう勉強すべきかという考え方を述べ、次に問題をどのように解くべきか具体的な話へ進み、その後はさらに具体的な話として問題を解くときのアプローチを紹介していきます。
そして最後に紹介したアプローチ方法を使って問題を解く方法を説明していきます。著者は数学の専門家ではありませんが、現在は個別指導塾の塾長という塾で数学を教える経験をされているようで、その経験がいかされた内容となっています。
前半部分の内容では例えや著名人の引用も分かり易くなされており、塾講師らしいなと感じさせる点がありますね。
オススメポイントとオススメしにくいポイント
この本のおすすめポイントですが「答えを読めばわかるのに数学の問題が解けない」「答えや定義は覚えられるけれどそれ以外にどう数学を勉強して良いのか分からない」そんな人の悩みを解決できる、というところです。
定義や数学の公式を覚えることで単純な問題は解けますが、なかなか応用問題は解くことができません。これはなぜかというと、実は式の一部を覚えているだけで、定義や公式の重要な本質を理解しておらず、他の定義や公式との繋がりも見えていないから、というのが本書の解答です。表面的な部分しか見ていないので、応用ができないわけです。
その解決策として、この本ではとにかく「覚えないこと」を重視しています。最低限の定義から出発して証明ができるようにする。本書では、これが定義や公式を論理的に結びつけていくために必要なことと考えています。
この論理的な結びつきの例として、物語を人に説明する時、不思議と一度しか見ていないものでも順序立てて説明できること、をあげています。
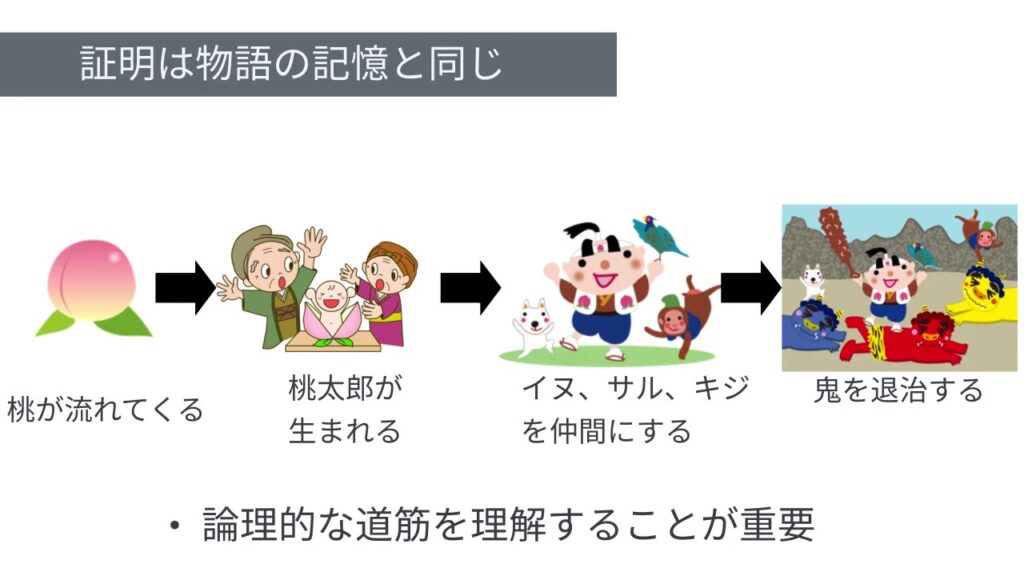
例えば、桃太郎のお話を話す時、毎回話し方は違ったとしても、上図で挙げるような本質的な部分はなんとなく覚えていて大きく変化しないですよね。このように本質となる部分を論理的に繋げるということが、数学では、定理や公式を導き出す証明になる、というわけです。丸暗記ではなく、道筋を覚える、というやり方であれば、忘れても流れで思い出せますよね。また、導き出すことはパズルを解くような知的好奇心を満たす面白さ、を与えてくれる点も重要です。楽しむことも学び続ける上では大事なことです。
この考え方を問題集を解く際にも応用することを薦めています。例えば、問題集で解けない問題があり、答えをみる時もその解答の行間にはどんな思考のプロセスがあるか、考えることを推奨します。式変形をするにしてもどんな目的や考えがあってそれを行っているのか、それを一つ一つ詰めることで初めて自分の論理力が向上するわけです。定理の証明についてもその背景にある思考のプロセスを突き詰めていくことが大事だ、と主張しています。
ここまで述べてきた「暗記をしない」「物語をつかむ」という勉強方法が本書一番の推しどころです。これは本の前半部分で述べられており、後半は数学的思考のプロセスに必要となる代表的な10のアプローチ方法について述べられています。具体的な内容は次のようなものです。
「次数を下げる」
「周期性を見つける」
「対称性を見つける」
「逆を考える」
「和よりも積を考える」
「相対化する」
「帰納的に思考実験する」
「視覚化する」
「同値変形を意識する」
「ゴールからスタートをたどる」
(「大人のための数学勉強法」より)
何となくこれだけみても数学をある程度やっている人なら雰囲気はわかると思いますが、その詳細な具体例は本書に収められていますので、ぜひ気になる人は参考にしてみてください。
さて、ではお勧めできないポイントですが、「高校数学まである程度できる人には後半の実例が蛇足になりうる」というところでしょうか。前半の内容は非常に本質を突いた鋭い内容だと思うのですが、後半の実例は数Ⅰベースなので難易度的にも簡単なものが多かったり、前半の本質を突いた内容に比べ、少しアンバランスな感じがしました。
まとめ
答えや公式の暗記だけでどうして数学の問題が解けないの?という疑問に真正面から答えてくれる貴重な本でした。大人のみならず中高生にも必要となる内容だと思いますので、数学が苦手でしょうがなかった高校生時代に読んでいれば、、と悔やまれます。数学に関して苦手な気持ちがある人は前半だけでも読んでみることをお勧めします。
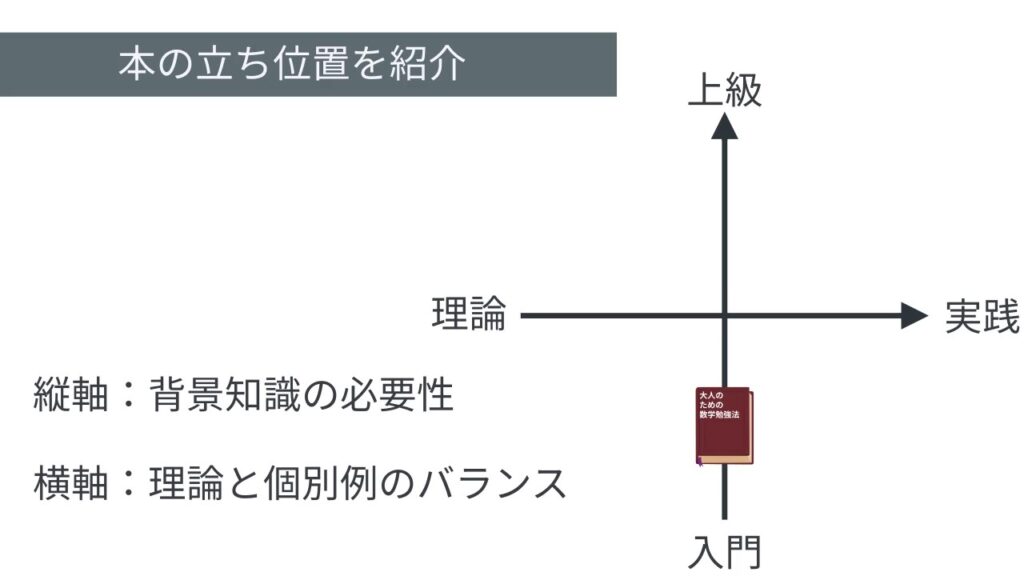
この本の立ち位置ですが、高校数学レベルの話しか出てきませんので入門書寄りといえます。理論と実践については前半は理論的な一般化した話、後半は具体例ですので中間あたりに位置していそうですね。バランスの良い入門書、と言えると思います。















コメントを残す