さて、濃密な第3章の内容からバックドア基準、フロントドア基準の紹介をしていきます。
目次:
バックドア基準
まず前回までの記事で観察された結果から介入による効果を推測するには、その変数の親となる変数の集合で調整すれば良いことが分かりました。
ところが、その親の集合全てがわかるわけではありません。現実問題として調べたい介入を促すような原因を全て知るのは不可能でしょう。観察されるデータには限りがあるわけです。
そこで、登場するのがバックドア基準です。
この基準を満たす変数の集合で条件付けすることができれば、介入による効果を観察データから推測することができる、というものです。
定義は次のように説明されています。
非巡回的有向グラフGにおいて変数の順序対(X,Y)が与えられたとき、変数の集合Zに含まれるいかなるノードもXの子孫ではなく、かつXとYの間の道でXに向かう矢線を含むようなものすべてをZがブロックするとき、Zは(X,Y)についてバックドア基準を満たすという。
『入門統計学的因果推論』
このままだと分かりにくいので実際にDAGを用いた例を見てみましょう。以下のようなDAGでバックドア基準を満たすのはどれでしょうか。
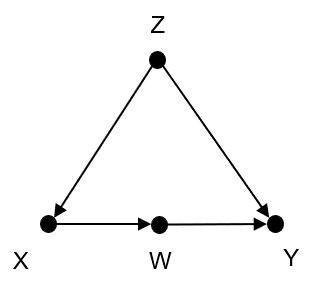
先ほどの定義を読みながら考えますと、まず「いかなるノードもXの子孫ではない」ということなので、この図の中でWはそれを満たしません。
続いて「XとYとの間でXに向かう矢線を含むようなものすべてをブロックする」という条件で、Zは条件を満たします。Zは分岐点であるため条件付けした場合、全てをブロックできることが確認できます。つまり、変数Zがバックドア基準を満たすわけです。
バックドア基準を満たしているZについて調整化公式を用いれば、Xの親全てについて条件付けしなくても、doオペレータで表現された介入による効果を推定できるので
となるわけです。
上記のDAGを使って具体的な例を考えてみます。
ある薬(X)は血圧を下げること(W)で脳梗塞の発症予防効果(Y)を持つと推測され、脳梗塞の既往がある人(Z)は薬を飲んでいる可能性が高く、また脳梗塞の再発もしやすいとしてみますと上記のグラフは以下のように当てはめられます。
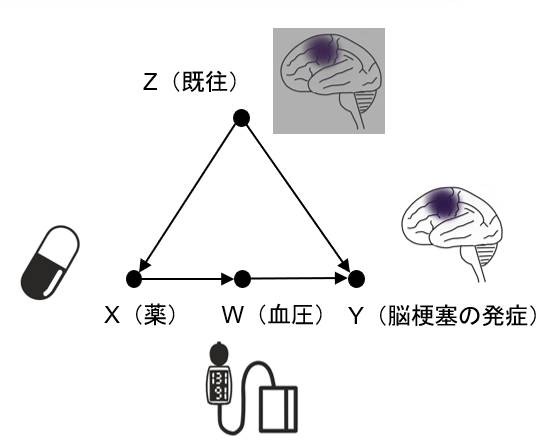
そうすると、薬による介入での変化を知りたい場合、上記の条件に沿ってバックドア基準を満たしているZについて調整すれば良いことになります。これはいわば脳梗塞の既往のある人・ない人に層を分けて比較していることと同じですので、均一な条件下で比較できていることが納得できます。
フロントドア基準
もう一つの有用な基準として書かれているのがフロントドア基準です。
先ほどのバックドア基準において観測されないデータが存在する場合、調整がどうしてもできずにバックドアを閉じられないことがあります。
本書で用いられている例が喫煙と肺がん、遺伝子型の話です。
通常、喫煙→肺がんという因果関係がありそうと思うわけですが、タバコ業界が「喫煙をしやすい遺伝子型の人が肺がんにもなりやすい」という交絡因子があると主張していた、と書かれています。すごい理論ですね・・・。
確かに全ての人の遺伝子を調べるわけにもいかず、そもそもその遺伝子が喫煙をしやすいかどうかの証明なんてこともできません。観測できない交絡因子であり続けるため、解決できないわけです。
そこで登場するのがフロントドア基準です。
数式的な理解としては結構複雑です。まず、X,Y,Z,Uの四つが以下のようなDAGになっていると考えてみます。X(喫煙)、Z(タールの蓄積)、Y(肺がん)、U(遺伝子的要因)であると考えてみます。Uは直接的に得られない未知のデータで、他は観測可能なデータとみなします。
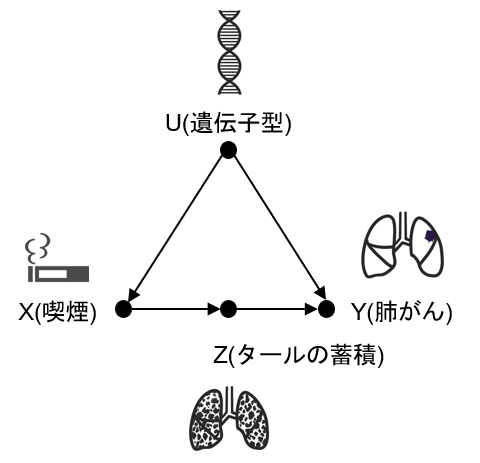
単純にバックドア基準で考えるとUがその基準を満たしていますが、未知のデータであるが故にUでの調整はできません。ですが、DAGをうまく使えば、実はXによる介入の効果を測定できるのです。
まずdoオペレータを使った同時確率を求めると以下のようになります。
\(P(Y=y, Z=z, U=u|do(X=x))=P(Y=y|Z=z, U=u)P(Z=z|X=x)P(U=u)\)
最終的に求めたいのは\(P(Y=y|do(X=x))\)ですので、不要であるZとUを足し合わせます。
\(P(Y=y|do(X=x))=\sum_zP(Z=z|X=x)\sum_uP(Y=y|Z=z,U=u)P(U=u)\)
ここで、前半部分の\(\sum_zP(Z=z|X=x)\)はいずれも観測可能なデータなので、計算可能です。問題は後半のUを含む部分です。
以下の経路(Z→Y←U→X)について考えてみます。Uは分岐路となっているためXで調整できればYへの影響をブロックできることがわかります。よってなんとか式の後半部分についてXによる調整をしてUを消去できるように考えていきます。
\(\sum_uP(Y=y|Z=z,U=u)P(U=u)\\=\sum_x\sum_uP(Y=y|Z=z,U=u)P(U=u|X=x)P(X=x)\\=\sum_x\sum_uP(Y=y|Z=z,U=u,X=x)P(U=u|X=x,Z=z)P(X=x)*\\=\sum_xP(Y=y|Z=z,X=x)P(X=x)\)
*Z,Uで条件付けした時XとYは独立、Xで条件付けした時ZとUは独立であるため
となりますので、無事Uを消去することができました。ここのXは全て足し合わせてしまうので前半部分のXと異なるものとしてX’と記載して、前半後半部分の式を合わせますと
\(P(Y=y|do(X=x))=\sum_zP(Z=z|X=x)\sum_{x’}P(Y=y|Z=z,X=x’)P(X=x’)\)
以上のフロントドア基準の条件を一般化すると以下のような表現となります。
1.ZはXからYへの有向道をすべてブロックする
2.XからZへのバックドアパスは存在しない
3.ZからYへのすべてのバックドアはXによりブロックされている
『入門統計学的因果推論』
X,Z,Yの間で他にバックドアパスが存在してしまうとこの調整がうまくいかなくなるので注意が必要ですね。
さて、3章は他に媒介変数や傾向スコア、逆確率重み付けなどの紹介があり、4章では反事実の重要な話になっていくのですが、ちょっと正直深堀りするには情報量も多くて知識も不足してますので、DAGに関連した話題に留めて『入門統計学的因果推論』の紹介は一旦ここまでとします。数冊因果推論の本を書い足したので、他の本も読み進めながらまた戻って来たいと思います。
参考文献:















コメントを残す