前回記事に引き続いて指数型分布→一般化線形モデル(GLM)の流れを備忘録としてまとめました。
まずはモデルの構築から。
モデルの構築手順
- \(\displaystyle y_i\) の分布(自然指数型分布)を決める
- 線形予測子 \(\displaystyle \eta_i = \beta x_i + \alpha\) を定める
- \(\displaystyle \eta_i = g(\mu_i)\) としてリンク関数を設定する
従属変数yが一体どんな分布を取るかを仮定して、さらにその従属変数yの確率分布のパラメータが線形予測子によってどのように説明されるかを組み立てる、というのがGLMのモデルの構築方法です。
例えば正規分布であれば以下の様に構築されます。それぞれyの分布のとりうる値に応じて適切なリンク関数があります。例えばyがポアソン分布であれば負の値は取らないので、リンク関数はexpを使った指数関数になる、などですね。
モデルの例
- \(\displaystyle y_i \sim \mathcal{N}(\mu_i, \sigma^2)\)
- \(\displaystyle \eta_i = \beta x_i + \alpha\)
GLMで扱える代表的な分布
GLMでは指数型分布族を扱うことができ、主には以下の様な分布が含まれます。メジャーな確率分布はカバーされていますね。
- 正規分布(normal)
- 二項分布(binomial)
- ポアソン分布(Poisson)
- ガンマ分布(gamma)
- 負の二項分布(negative binomial)
- 幾何分布(geometric)
- 逆ガウス分布(inverse Gaussian)
GLMが成立するための仮定
GLMを成立させるためにはまず観測値 \( y_i \) が以下を満たすことが前提です。
- 独立に観測されている(independent)
- 同じ分布に従っている(identically distributed)
いわゆる、\( y_1, y_2, \dots, y_n \) は iid(独立同分布)である、ということです。
これが成り立たない場合(例:観測間に相関があるなど)は、GEE(Generalized Estimating Equations)など相関を加味した他の枠組みが必要となります。
過分散とPearsonのカイ二乗統計量
GLMが実際にうまくフィットしているかどうか、モデルのあてはまりを検証するためにPearsonのカイ二乗統計量を用いて分散の大きさを評価することができます。従属変数yとその平均μ、分散Vを用いると以下の式はカイ二乗分布に従うと言えます。
\[
\sum_{i=1}^n \frac{(y_i – \hat{\mu}_i)^2}{\text{Var}(\hat{\mu}_i)} \sim \chi^2(n – p)
\]
ここで:
- \( \hat{\mu}_i \):予測された平均
- \( p \):推定されたパラメータの数
- \( n \):サンプルサイズ
です。
この統計量の期待値は理想的には:
\[
\mathbb{E} \left[ \sum_{i=1}^n \frac{(y_i – \hat{\mu}_i)^2}{\text{Var}(\hat{\mu}_i)} \right] = n – p
\]
となるはずです。しかしながら実際の観測値の分散が理想より大きい場合、分子がより大きくなります。
過分散の検出
比率として書き直してみると
\[
\frac{1}{n – p} \sum_{i=1}^n \frac{(y_i – \hat{\mu}_i)^2}{\text{Var}(\hat{\mu}_i)} > 1
\]
なら、過分散(overdispersion)の疑いがあるといえます。
この状況はモデルが仮定する分散より、実際のデータのばらつきが大きいと言えます。
こうした状況を起こす原因としては説明変数の取りこぼしや分布のミスマッチ、非独立性などがあります。
続いてGLMが成立する場合の式についてみていこうと思います。
指数型分布族の形式
GLMでは、従属変数の分布が次の形をとると仮定します。
\[
f(y_i) = h(y_i) \exp\left[ \theta_i y_i – A(\theta_i) \right]
\]
これは前回の記事でまとめた指数型分布族の一般的な式です。
尤度関数とその導出
ここから最尤推定を行う場合の一般式を導いてみようと思います。
まず対数尤度関数は以下のように書けます。
\[
L(\mu_i) = \log \prod_{i=1}^n f(y_i)
= \sum_{i=1}^n \log f(y_i)
= \sum_{i=1}^n \left[ \theta_i y_i – A(\theta_i) + \log h(y_i) \right]
\]
スコア関数(\( \beta \) に関する微分)
続いてβに関して微分し、スコア関数(=対数尤度の \(\beta\) による微分)を求めますが、正規化項A(Θ)は自然パラメータΘの関数ですので、微分は連鎖律を使う必要があります。
\[\frac{\partial L}{\partial \beta}= \sum_{i=1}^n \left( y_i \cdot \frac{\partial \theta_i}{\partial \beta} – \frac{\partial A(\theta_i)}{\partial \theta_i} \cdot \frac{\partial \theta_i}{\partial \beta} \right)\\= \sum_{i=1}^n (y_i – \mu_i) \cdot \frac{\partial \theta_i}{\partial \beta}\]
ここで、\(\mu_i = A'(\theta_i)\) を使いました。
\(\theta_i\) は \(\mu_i\) を通じて \(\eta_i\) に依存するため、連鎖律により次のように表せます:
\[\frac{\partial L}{\partial \beta}= \sum_{i=1}^n (y_i – \mu_i) \cdot\frac{\partial \theta_i}{\partial \mu_i} \cdot\frac{\partial \mu_i}{\partial \eta_i} \cdot\frac{\partial \eta_i}{\partial \beta}\]
\( \partial \theta / \partial \mu \) の評価
指数型分布の性質から:
\[
\frac{\partial \mu_i}{\partial \theta_i}
= \frac{\partial}{\partial \theta_i} \int y_i h(y_i) \exp\left( \theta_i y_i – A(\theta_i) \right) dy_i
= Var(y_i)\\
\quad \frac{\partial \theta_i}{\partial \mu_i} = Var^{-1}(y_i)
\]
スコア関数の最終形
上記の関係を代入すると:
\[
\frac{\partial L(\beta)}{\partial \beta}
= \sum_{i=1}^n (y_i – \mu_i) \cdot \text{Var}^{-1}(y_i) \cdot \frac{\partial \mu_i}{\partial \eta_i} \cdot \frac{\partial \eta_i}{\partial \beta}
\]
各項の微分関係
今回の例ではリンク関数が恒等リンク関数という単純な形であるため、他の微分の項においても比較的簡単にまとまります。
- リンク関数より:
\[
\eta_i = g(\mu_i) \Rightarrow \frac{\partial \mu_i}{\partial \eta_i} = g’^{-1}(\eta_i)
\] - 線形予測子より:
\[
\eta_i = \mathbf{x}_i^\top \beta \Rightarrow \frac{\partial \eta_i}{\partial \beta} = \mathbf{x}_i
\]
最尤推定条件
最後にスコア関数をゼロとおいて最尤推定を行うことでβを求めます。
正規分布では最終的に正規方程式になりますが、ポアソン分布などだと解析解が求められないので、ニュートンラフソン法など反復計算を用いて解く必要が出てきます。
この辺の具体例の計算は次回の記事で書いていきます。
\[
\sum_{i=1}^n (y_i – \mu_i) \cdot \text{Var}^{-1}(y_i) \cdot \frac{\partial \mu_i}{\partial \eta_i} \cdot \frac{\partial \eta_i}{\partial \beta}
= 0
\]
参考文献
Hardin, James W., and Joseph M. Hilbe. Generalized estimating equations. chapman and hall/CRC, 2002.




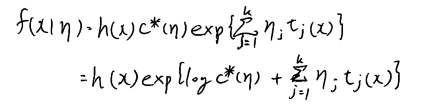







コメントを残す