本日も統計問題の続きを。
5章問3はどうも何度か解答見ても納得できなかったので
問4にいきます。
F分布の何乗かした期待値を求める問題です。
3章問18でみられたχ2乗分布の特徴を用いて解きます。
上の半分がその説明となっています。
(※分子のガンマはv+n/2の間違いでした)
Xがχ2乗分布に従う場合、そのv乗の期待値(vは非負の実数)は
下図のガンマ関数で表されます。
ここで式の変形途中のxを見てみると
n/2+v-1 乗されています。
つまりこれが負でなければガンマ関数として成立するので
仮にvが負であってもn/2より小さければ成立します。
それを利用して

と導かれます。
ちなみにですが、初回これを解くときに、愚かにも
E[1/T] = 1/E[T] だなんて考えだしてしまったのですが
これは当然×。
サイコロの例で考えればすぐわかりますが、目の数をXとして
1/E[X] = 2/7
E[1/X] = (1+1/2+1/3+1/4+1/5+1/6)×1/6 = 49/120
全然一致しませんね。
最後の式変形は Γ(m+n/2)が打ち消しあうことで変形できます。

今回の問題で疑問なのは
この3章の問18の知識っていうのは割と必須な公式なんでしょうか、、、?
ということ。
パッと出てくるものではないように思えてきます。

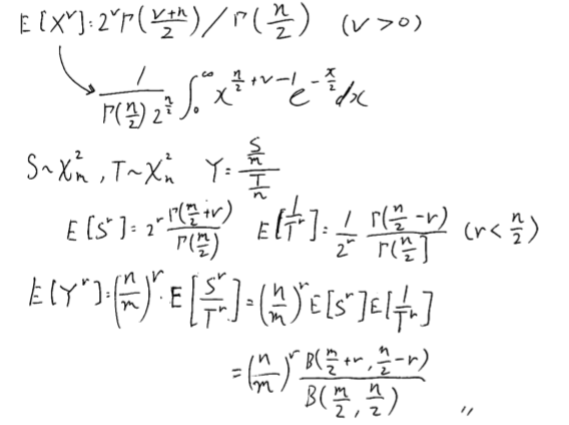
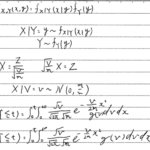













コメントを残す