*今までに解いた問題の解答解説まとめページを作りました(2020.9.15追記)↓
現代数理統計学の基礎 解答・解説まとめ – 脳内ライブラリアン
今回は6章。
5章は実は以前解いていたので復習がてら載せていましたが
今解いてる6章から順番に並行して載せていきます。
問1はひたすらに様々な分布で十分統計量を書いていくだけの問題なので
問2から。
十分統計量と最尤推定量の問題ですね。

同時確率密度関数をまず書きます。
たいていの場合はi.i.d.(互いに独立)なので
単純にすべての確率密度関数の積で表現できます
あとは自然対数eとlogを用いて
母数(この問題ではθ)とXiの関数を表現できればOK。
因子分解定理に従って十分統計量が出ます。
続いて最尤推定量ですが、まず対数尤度関数をとります。
対数尤度関数を母数で偏微分し、0になるような値を求めます。
いわゆる最尤法ですね。

最尤推定量のθhatが出ます。
ξ は θ の関数なので θ の最尤推定量を用いれば ξ の最尤推定量が出ます。
とここまではいいのですが、問題はその先。
最尤推定量の分散を続いて求めます。
logx1,2,3,….nの期待値や分散はすべて同じ分布に従い、かつ互いに独立なため
ひとまずX1についての期待値あるいは分散がわかれば、何とかなりそうです。
そこで-logX1をYとおいて期待値を計算します。

公式の解答はこんな細かい計算過程がないんですが
すぐに回答が出るような別の考え方があるんですかね、、?
ひとまず地道に計算したとしても =ξ という結果が出ます。
E[Y2乗]は省略します笑
これでVar(Y1)が出るので、

となります。


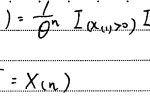
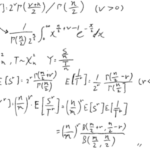












コメントを残す