引き続いて6章より問5です。
多項分布における最尤推定量の問題です。
パラメータがk個と多数ありますがやり方は比較的簡単です。
(1行目)多項分布の確率密度関数になります。
(2行目)対数尤度関数で表します
積が和に変換されるので下記の式になります。

そこからはp1~pkの確率総和が1であることを利用して
ラグランジュの未定乗数法を用います。
ラグランジュの未定乗数法ってなんやねんという人には
以下のリンクが説明がわかりやすいです。
高校数学の美しい物語
方程式の解になりそうなものをとりあえず導き出せる便利な式です。
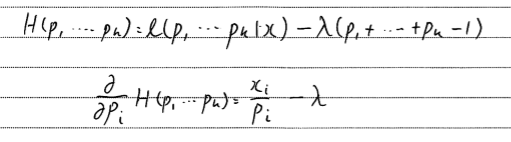
p1-pkのどれかで微分すれば、残るのは上記の式のみになります。
これを改めて制約式に代入して求まったλを代入して解を得ます。

ほかの問題でもラグランジュの未定乗数法が使われていたりするので
覚えておくと便利ですね。











コメントを残す