今回は脳梗塞診療に関わる臨床医師向けのせまいせまい話を通して、順序ロジスティック回帰分析の話を書こうと思います。
急性期の脳梗塞の論文って血栓回収にアルテプラーゼ、最近ではテネクテプラーゼと賑わいを見せ続けている分野だと思うんです。ただ、最近論文を読んでいて思ったのは、解析方法がわからん、、、という情けない話です。解析方法がよく理解できないので、効く効かないくらいは分かりますが、それ以上の結果の解釈がわかりません。
例えば今年中国から出た血栓回収+アルテプラーゼと血栓回収単独を比較したstudy。
Endovascular Thrombectomy with or without Intravenous Alteplase in Acute Stroke
Primary Outcomeはmodified Rankin Scaleと書いてあるのですが、outcomeは共通オッズ比。このオッズ比は一体何の何に対してのオッズ比なのか?これは以前同じ疑問を血栓回収の有名なtrialであるMR. CLEANを読んだ時も思いました。
A randomized trial of intraarterial treatment for acute ischemic stroke – PubMed(今はフリーで読めます)
実はどちらも順序ロジスティック回帰分析(ordinal logistic regression)という方法を使っているのですが、あまりよく使われる手法ではないので、今まで分かりませんでした。
で、この解析方法はそもそもどういう方法なのか、加えて何故このような手法を使うのか。調べてみました。この解析が気になる方は「ロジスティック回帰分析」のところから読んでください。
目次:
脳梗塞のアウトカムの特殊性
そもそも急性期脳梗塞治療のアウトカムでなぜこのような特殊な手法が使われるのか。それはひとえに脳梗塞で起きることが他の疾患と比べて特殊であることが原因です。
まず、脳梗塞は「治る、治らないだけの病気ではない」こと。もちろん麻痺症状がなくなって、完治もありますが、重度な麻痺以外に、動くけれど生活は自立できない、動けて生活はできるけれど仕事は微妙、などなど様々な段階に分かれます。そしてこれらの重症度が「連続変数として数値化できない」ことも特徴です。もちろんmodified Rankin Scale(mRS)や、NIHSS scoreなどはありますが、これらはあくまで質的変数(=非連続変数)です。1ポイントの差は統一されていません。
また、脳梗塞は基本的に「死ぬ、死なないの病気でもない」ことも特徴です。もちろん脳底動脈閉塞や広範な脳梗塞による脳ヘルニアなど亡くなられる方もいるわけですが、アウトカムを「死亡」にするほど多数ではありません。
こういった事情から普通の2値解析がしにくい点が脳梗塞の特徴です。この辺りはまた後述します。
まずは最初に挙げたstudyで使われている順序ロジスティック回帰分析について説明していきます。
ロジスティック回帰分析
そもそも順序ロジスティック回帰分析の話の前に、ロジスティック回帰分析について説明してみます。
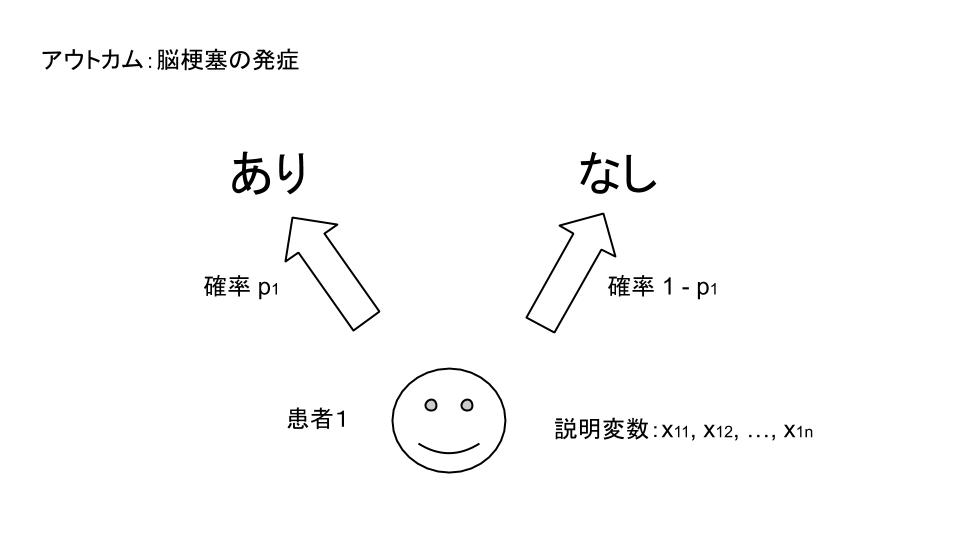
ロジスティック回帰分析とは被説明変数が0-1の範囲に収まるように説明変数の式が設定される回帰分析のことです。もっと単純に言えば、反応あり/なしの2値の結果の確率を予測する回帰分析です。脳梗塞を例にした場合を図で描くとこんなイメージです。

説明変数(11は患者1における1つ目の説明変数、という意味です) をもつ患者さんが脳梗塞を発症する確率
を予測する式をつくるのがロジスティック回帰分析です。
実際の式は定数βを含めて、以下のようになります。
expの中身が∞になると確率pは1になり、expが-∞になると確率pは0になることが確認できます。
回帰分析はこの分母にあるβを算出するのが目的なので、logを使って変形して以下の式から計算していきます。
ここで説明変数に掛け算するは偏回帰係数(β coefficient)と呼ばれます。説明変数が0もしくは1の2値変数である場合は
がオッズ比(odds ratio)となります。
これは求めたい確率のオッズが上記の式を変形して
となることからも 何となく理解できるかと思います。
順序ロジスティック回帰分析
では、順序ロジスティック回帰分析(ordinal logistic regression)とは何なのか。
上述したように脳梗塞のアウトカムは「連続変数でない」かつ「2値変数ではない」ので、連続変数を扱う重回帰分析や2値変数を扱うロジスティック回帰分析は使えません。そこで使われるのが順序ロジスティック回帰分析です。
順序ロジスティック回帰分析は、被説明変数が質的変数である場合に使われる回帰分析手法です。
実際に最初に紹介したstudyで使われているのと同様に、アウトカムをmRSとして考えてみます。
mRSでは0-6までの7段階の尺度があります。まず、それを2つに分けてロジスティック回帰分析の式を想定します。0を反応あり、1-6を反応なし、として、さっきと同様に考えてみます。図にするとこんな感じです。

式は
ですね。
説明変数(iは患者番号が入る)を治療あり=1, 治療なし=0として考えてみると
は治療によってmRS=1-6の人が、mRS=0に変わるオッズ比を表していることが分かります。
同様にしてmRS 0-1を反応あり、2-6を反応なし、として再度ロジスティック回帰分析の式をたてます。図はこんな感じです。

式は
となります。
このとき、定数項が
に変更された以外、偏回帰係数は一緒です。つまりどのような区分けにしようと治療によるオッズ比は変わらない、という前提に立っています。
なので今回もは治療によってmRS=2-6の人が、mRS=1-2に変わるオッズ比を表しています。
また、定数項の差が最初のモデルとの唯一の違いであり、この違いは二つの確率のオッズ比が比例していることを前提にしています。式で表すと
という形になります。これは比例オッズモデルと呼ばれます。
この区分けをあとはひたすら続けます。0 vs 1-6, 0-1 vs 2-6,… , 0-5 vs 6と計6回にわたります。すべての式で偏回帰係数が同じ、かつ比例オッズモデルが成り立つとみなして、実際の試験のデータを用いて、最尤法(もっともパラメータβがとりうる確率が高くなる値をもとめる方法)で偏回帰係数βを算出します。
治療介入の有無を説明変数に設定したので、
が治療による色々な区分け全ての共通のオッズ比、ということで共通オッズ比(common odds ratio)が求められます。
これが一番初めに疑問だった脳梗塞のstudyでmRSをアウトカムとして順序ロジスティック回帰分析をしたときに、求まるのが共通オッズ比である流れです。
ちなみに、この解析が前提としている「どのモデルでも治療のオッズ比が同じ」ということや「比例オッズモデル」が成り立つのかどうかは個人的には疑問です。
以上の話は参考文献からかき集めてきた情報で、まとめてあるような成書や文献がなかったので、もし間違っている点があったらご指摘お願いします。
次になぜこのようなやや面倒な解析方法をやっていく流れになったのか、2007年とちょっと古いレビューを読んでみます。
続きはこちら
急性期脳梗塞の臨床試験の解析方法が分かりにくすぎるので、勉強した話②
急性期脳梗塞の臨床試験の解析方法が分かりにくすぎるので、勉強した話③
(2021.06.28追記 医学論文の読み方関係の記事はこちらにまとめました)
参考文献:
高度過ぎて理解が追いつきませんが、端折ったりせず、しっかりとした内容の詰まったサイトです
Saver JL. Novel end point analytic techniques and interpreting shifts across the entire range of outcome scales in acute stroke trials. Stroke. 2007;38(11):3055-3062. doi:10.1161/STROKEAHA.107.488536
過去の脳梗塞のtrialの問題点と解決策となる解析手法をまとめたレビューです
Bath PM, Lees KR, Schellinger PD, et al. Statistical analysis of the primary outcome in acute stroke trials [published correction appears in Stroke. 2012 Sep;43(9):e100]. Stroke. 2012;43(4):1171-1178. doi:10.1161/STROKEAHA.111.641456
こちらも過去のtrialと最近の解析手法をまとめたレビューです








コメントを残す