2016年、2019年と出題されているノンパラメトリック法の検定について簡単にまとめておきます。
符号検定とは
符号検定は1標本に対して行われるノンパラメトリック検定です。ある対応するデータの差が正であれば1、負であれば0として、それをデータの数だけ足し合わせたものを検定統計量\(S_n\)とします。差が明らかにあるのであれば、\(S_n\)は大きくなるはずなので、差がないとした帰無仮説下での、その確率を計算して有意かどうか調べます。
具体例で考えてみる
実際の例をみるとより分かりやすいので、適当な例を出してみます。(この試験にノンパラメトリック法が適切かどうかはひとまずおいておきます)
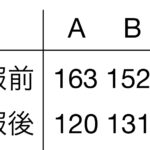
5人の被験者に降圧剤を内服してもらい、収縮期血圧が内服前後で以下のように変わったとしてみます。

この時、符号検定を5%有意差の片側検定で行ってみます。
まず、(内服前)ー(内服後)で下がっているものを正として、みてみると以下のように5例中4例で下がっていることが分かります。

ここで、帰無仮説下ではデータ間に差はないはずなのでこうした事象が起きる確率は、被験者5名について1/2の確率で差があるorないということが起きるような二項分布Bin(5, 1/2)に従います。
よって、例えば \( S_n = 4 \) となるような事象は
\[
P(S_n = 4) = \frac{1}{2^5} {_5C_4}
\]
の確率で起きることがわかります。
有意差を考えるには\ ( S_n = 4\ ) 以上の数値を考えれば良いので、
\[
P(S_n \geq 4) = \frac{1}{2^5} {_5C_4} + \frac{1}{2^4} {_5C_5} \
= 0.1875
\]
となり、有意差がないことがわかりました。
符号検定の一般的な式
上記の例を一般化してきちんと書くと、変化前後のデータの数値 ( X ) が従う分布関数の中央値をそれぞれ、\( \Delta_0, \Delta \)、とすると
帰無仮説\ ( H_0: \Delta = \Delta_0 \) あるいは\( P(X > \Delta_0) = P(X < \Delta_0) = \frac{1}{2}\)
対立仮説
\[
H_1: \Delta \neq \Delta_0
\]
となります。
片側検定では対立仮説が
\(\Delta\gt\Delta_0あるいはP(X\gt\Delta_0)\)
もしくは
\(\Delta\lt\Delta_0あるいはP(X\lt\Delta_0)\)
となります。
先程の例と同様に片側検定で上の対立仮説を用いたものを考えてみます。
帰無仮説下においては上記のように、差が出る確率は均等にランダムで 1/2 になるはずなので、検定統計量 ( S_n ) の数値以上となるのが、どの程度の確率なのかを求めて、有意差があるかどうかを判定します。
よって式は
\[
P(S_n \geq s_n) = \frac{1}{2^n} \sum_{i=1}^n {_nC_i}
\]
となり、これによって検定します。
サンプル数が多い場合の正規近似
サンプル数が多い時には、組み合わせの数を直接求め続けるのは大変なので、正規分布への近似を行います。
\( S_n \) は二項分布 \( \text{Bin}(n, 1/2) \) に従うので、期待値は \( n/2 \)、分散は \( n/4 \) となります。
よって
\[
\frac{s_n – \frac{n}{2}}{\sqrt{\frac{n}{4}}} = Z
\]
は標準正規分布に近似されます。
標準正規分布表を用いてこの部分の確率を計算することで、先程の ( P(S_n \geq s_n) ) などを求めることができます。
参考文献:
最近買いましたが、理論的な背景をしっかり説明していて、納得できる本です。若干理解が難しいところもあります。















コメントを残す