超久しぶりにこのテーマで記事を書きますが、臨床試験を読んで意味がよく分からなかった統計的内容を頑張って理解してみようという趣旨の記事です。
今回は負の二項回帰モデルについて気になったところだけ簡単に触れる浅い内容となっております。
脳神経内科領域では多発性硬化症の第3相試験など再発率を比較した論文で負の二項回帰モデル(negative binomial regression model)がよく使われています。
最近ちょうどofatumumabの使用を検討する機会がありまして、第3相試験の論文をみていたのですが、そのprotocolには負の二項回帰モデルが登場しています。
Ofatumumab versus Teriflunomide in Multiple Sclerosis|NEJM
(こちらからsupplementary materialへいき、その中のprotocol page 104にモデルについて書かれています)
ではなぜ負の二項回帰モデルを使うのでしょうか。
負の二項分布というと、確率pで成功、1-pで失敗する事象がn回成功するまでにx回失敗するときの確率分布を示すNB(n,p)というイメージでしたので、さっぱりよく分からなかったのですが、調べた結果なんとなくイメージがつかめたのでメモ代わりに書いていこうと思います。
臨床試験の概要
この試験の内容は多発性硬化症患者さんに対してofatumumab(ケシンプタ), teriflunomide(日本未発売)の2つをランダム割付し、年間再発率を比較した二重盲検試験となっています。
多発性硬化症が他の疾患と異なるところは1回再発したらそれで打ち切り、というような脳梗塞などとは違い、短期間でも何回も再発する可能性があるため、アウトカムが0以上のカウントデータとなることが特徴的です。それゆえに単純なCox比例ハザードモデルでは検証しにくいものと思われます。
ポアソン分布によるモデル
まず、関連する点としてポアソン分布によるモデルに触れておきます。
ポアソン分布は離散的なカウントデータで0以上しかとらない場合に使用されます。確率分布から基本的な特性をみていきます。
ポアソン分布の期待値と分散
ポアソン分布の確率密度関数は以下で表されます。一定時間内にイベントが起きる回数をxとして
\(P(X=x)=\frac{\lambda^x}{x!}e^{-\lambda}\)
となります。期待値と分散を計算すると
\(E[X]=\lambda, V(X)=\lambda\)
となり、期待値と分散が一緒の値になります。
ポアソン分布の形状を実際にpythonで見てみる
同じ離散的カウントデータでありながら、ポアソン分布ではなく負の二項分布を使う必要性についてネットで調べると「過分散が問題となる(分散が期待値より大きいと困る)」「0に多いデータに弱い」ことがよく記されています。何がどう具体的に問題なのか書いてあることが少ないのでより詳しくみてみます。
先ほどみたようにポアソン分布は期待値と分散が一致します。よってλ一つのパラメータで分布を制御しており、xのイベント数が増えるとすると必然的に分散も大きくなるため散らばりが大きくなります。
実際にpythonでλの変化によるポアソン分布の広がりをみてみましょう。
Google Collaboratoryを使いますので、みなさんもコピーしてλのパラメータを好きにいじってみると面白いです。今回はE[X]=λ=1,3,5,7,10で出力してみました。コードは以下になります。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータのリストを定義します
lambda_values = [1, 3, 5, 7, 10] # 異なるλ(ポアソン分布の平均)値を試してみましょう
# ポアソン分布を描画します
x = np.arange(0, 20) # x軸の値を設定します
plt.figure(figsize=(10, 6)) # グラフのサイズを調整
for lam in lambda_values:
poisson_dist = poisson.pmf(x, lam) # ポアソン分布を計算します
plt.plot(x, poisson_dist, label=f'λ={lam}')
# グラフの装飾
plt.title('Poisson Distribution')
plt.xlabel('X')
plt.ylabel('Probability')
plt.legend()
plt.grid()
# グラフを表示
plt.show()λの値に応じた出力結果は以下のようになります。
poisson_and_negativebinomial.ipynb
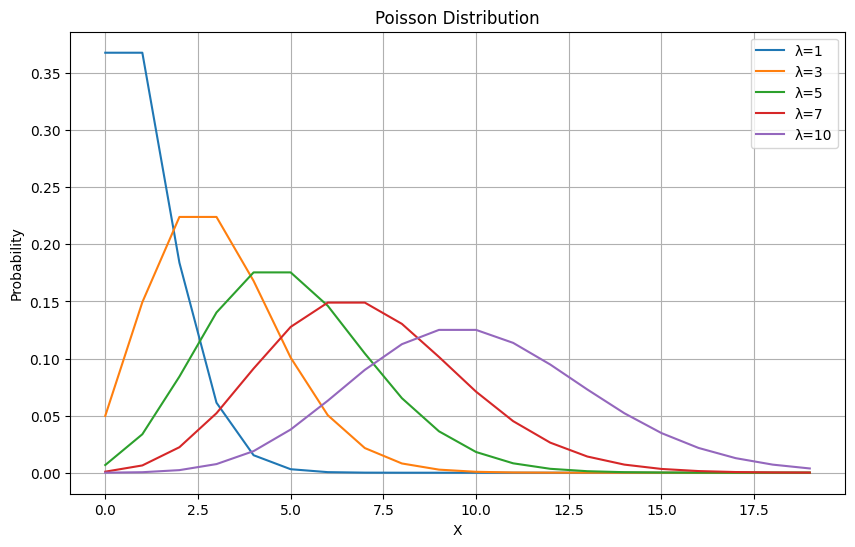
λが増えると徐々になだらかになっていくのが分かるでしょうか。このことから期待値が上がると0に近いデータが多い場合そぐわなくなる可能性があります。
負の二項分布によるモデル
では負の二項分布はどうなのでしょうか。冒頭でも述べたように教科書的には負の二項分布は「確率pで成功、1-pで失敗する事象がn回成功するまでにx回失敗するときの確率分布」をパラメータn,pを用いて以下のように表現します。
\(P(X=x)=_{n+x-1}C_x p^n(1-p)^x\sim NB(n,p)\)
ここで先ほどの臨床試験のプロトコールの内容をみてみると年間発症率をλ、フォローアップ期間をT、過分散パラメータをκとして
\(NB(\lambda T, \kappa)\)
となっています(添え字は省略)。この時点で「自分の知っていた負の二項分布と違う、、、」と取り乱していたのですが、結構このパラメータの表示方法もよくされるようです。実際のところパラメータの表現方法が異なっているだけで同じ分布ではあります。このパラメータは期待値と分散を表現するためのものとなっており、意味については以下で続けていきます。
負の二項分布の期待値と分散
NB(n,p)では期待値と分散は以下のようになります。
\(E[X]=\frac{n(1-p)}{p}, V(X)=\frac{n(1-p)}{p^2}\)
これをもう一つのパラメータの表現方法\(NB(\lambda T, \kappa)\)では平均値をμ(=λT:先ほどの例の場合)として分散は\(\mu+\kappa\mu^2)\)と表されます。
ここで分散がμよりも\(\kappa\mu^2)\)だけ大きくなっていることに注目です(κ>0)。先ほどのポアソン分布とは異なり、その分だけ過分散を表現することができます。
では続いて実際に負の二項分布の形状をpythonで見てみましょう。
負の二項分布の形状を実際にpythonで見てみる
では負の二項分布の形状を見ていきます。pythonのscipyなどのライブラリではNB(n,p)のパラメータ表示方法に基づいて入力をしますので、μとκを用いてn,pが表現できるようにしてみます。
まず
\(E[X]=\mu=\frac{n(1-p)}{p}\)
ですので
\(p=\frac{n}{n+\mu}\)
となります。続いて分散についても等式を立てると
\(V(X)=\frac{n(1-p)}{p^2}=\mu+\kappa\mu^2\\\frac{1}{p}=1+\kappa\mu\\p=\frac{1}{1+\kappa\mu}\)
これを先ほどの式に代入して
\(n=\frac{1}{k}\)
が得られます。
先ほどのgoogle colabの二つ目にこの式変形を使ったセルが入っています。
poisson_and_negativebinomial.ipynb
次のようなコードとなっています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import nbinom
# 平均の値のリストを定義します
mu_values = [1, 3, 5, 7, 10] # 異なる平均値を試してみましょう
kappa = 0.2 # κ
# x軸の値を設定します
x = np.arange(0, 20)
plt.figure(figsize=(10, 6)) # グラフのサイズを調整
for mu in mu_values:
# 負の二項分布のパラメータを計算します
n = 1 / kappa # パラメータnを計算
p = 1 / (1 + kappa * mu) # パラメータpを計算
# 負の二項分布を計算します
neg_binom_dist = nbinom.pmf(x, n, p)
# グラフを描画します
plt.plot(x, neg_binom_dist, label=f'μ={mu}, κ={kappa}')
# グラフの装飾
plt.title('Negative Binomial Distribution')
plt.xlabel('X')
plt.ylabel('Probability')
plt.legend()
plt.grid()
# グラフを表示
plt.show()平均値は先ほどと同様にしてκ=0.2, μ=1,3,5,7,10とします。すると
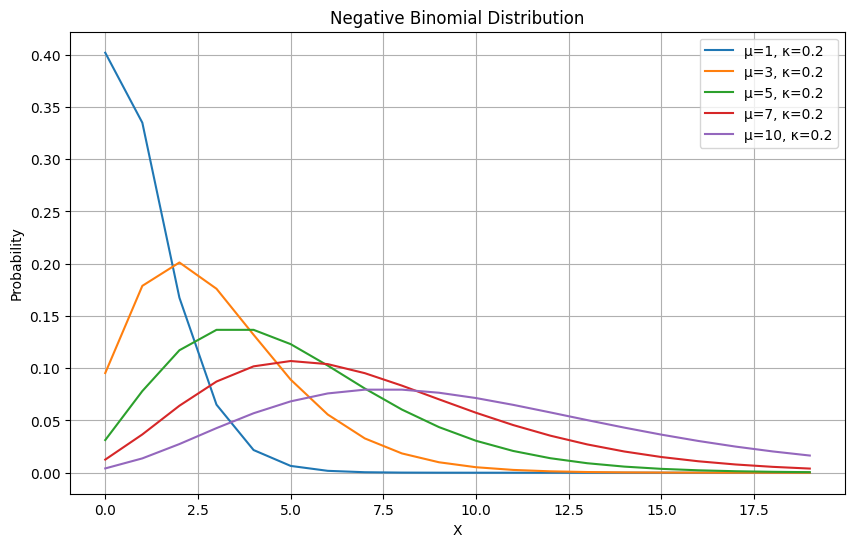
0に近い部分の確率が先ほどよりも高いことがわかります。期待値が上昇しても0の部分の確率の低下度合いは軽度です。これをみると「0が多いデータに強い」ということもわかりますね。
なお、先ほどの臨床試験ではイベント数が負の二項分布に従うことを利用しつつ、さらにデルタ法による近似を用いて両群での差を確率分布に落とし込んで、検定を行っています。またこの辺は別個の話となるので省略します。
おまけ:ポアソン分布と負の二項分布から標本抽出して歪度を比較してみる
「負の二項分布の方が左に寄ってんなあ」という雰囲気がありますので、ついでに標本抽出して歪度をチェックしてみます。平均値は5で揃えて、過分散パラメータκ=0.2としてみます。例として以下のような結果となりました。
ポアソン分布の歪度: 0.30 負の二項分布の歪度: 0.93
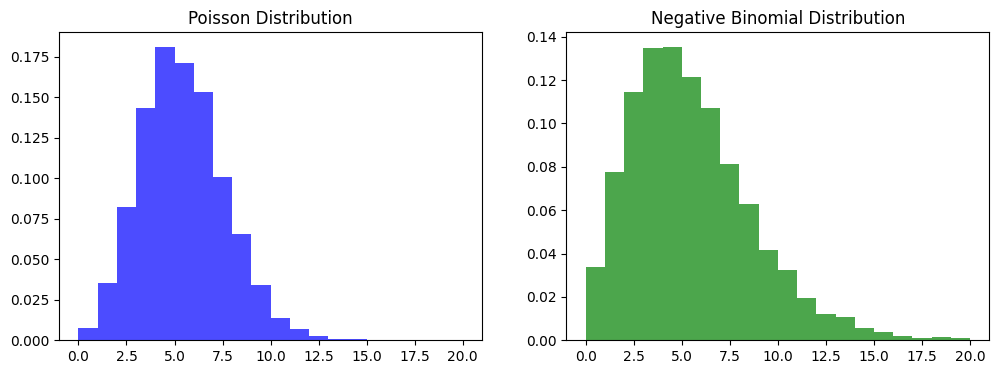
ほぼ間違いなく負の二項分布の歪度が大きく出てきますね。コードは以下のようにしました。
import numpy as np
from scipy.stats import poisson, nbinom
import matplotlib.pyplot as plt
# ポアソン分布からランダムな標本を生成して歪度を計算
def poisson_sample_and_skewness(mean, sample_size):
samples = poisson.rvs(mean, size=sample_size)
skewness = np.mean((samples - mean) ** 3) / (np.sqrt(mean) ** 3)
return samples, skewness
# 負の二項分布からランダムな標本を生成して歪度を計算
def negative_binomial_sample_and_skewness(n, p, sample_size):
samples = nbinom.rvs(n, p, size=sample_size)
mean = n * (1 - p) / p
variance = n * (1 - p) / p ** 2
skewness = np.mean((samples - mean) ** 3) / (np.sqrt(variance) ** 3)
return samples, skewness
# ランダム標本のサイズ
sample_size = 5000
# ポアソン分布のパラメータ
mean_poisson = 5
# 負の二項分布のパラメータ
n_nbinom = 5
p_nbinom = 0.5
# ポアソン分布から標本を生成して歪度を計算
poisson_samples, poisson_skewness = poisson_sample_and_skewness(mean_poisson, sample_size)
# 負の二項分布から標本を生成して歪度を計算
nbinom_samples, nbinom_skewness = negative_binomial_sample_and_skewness(r_nbinom, p_nbinom, sample_size)
# 結果を表示
print(f"ポアソン分布の歪度: {poisson_skewness:.2f}")
print(f"負の二項分布の歪度: {nbinom_skewness:.2f}")
# ヒストグラムでランダム標本を可視化
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.hist(poisson_samples, bins=np.arange(0, 21, 1), density=True, alpha=0.7, color='blue', label='Poisson Samples')
plt.title('Poisson Distribution')
plt.subplot(1, 2, 2)
plt.hist(nbinom_samples, bins=np.arange(0, 21, 1), density=True, alpha=0.7, color='green', label='Negative Binomial Samples')
plt.title('Negative Binomial Distribution')
plt.show()というわけで色々と遊んでみましたが、負の二項分布モデルが「過分散の問題に対応しやすい」「0が多いデータに適している」という点は理解できたように思います。実際の分布をパラメータを変えながら眺めるというのは理解の助けになって良いものですね。
ちなみに、今回のプログラミングに関してはChatGPTの全面的な助けを得ております。素晴らしい速度でプログラムを作れるので大変ありがたいのですが、計算についてはしれっと嘘にまみれていました、、、。使用の際はご注意を。
統計学をどんどん自分で学んで深めたい、という方へのおすすめ書籍をこちらのページの下部にまとめております。初心者向けのものから応用まで幅広く読んでいますので参考にどうぞ。














コメントを残す