最近、測度論と集合論の勉強が楽しくなってきたので、かつてよく分かってなかったボンフェローニ法による多重検定の補正について数式を考えてみます。例によって誤りがありましたらご指摘いただけますと幸いです。
分類上統計検定1級対策ページに入ってますが、多分出そうな内容ではありませんのでご注意ください(汗
ボンフェローニ法とは
ボンフェローニ法というのは多重検定の補正方法の一つです。いくつも同時に統計的仮説検定を行うと、少なくとも一つの検定でαエラーが起きる確率(ファミリーワイズエラー率 FWER; FamilyWise Error Rateと言われます)というのは必ず上がってしまいます。多重検定が抱えるこの問題は医療統計youtubeでも紹介しました。
そこで、多重検定を行う場合でもαエラーが起きる確率を抑える最も保守的な方法であるのが、ボンフェローニ法です。
ボンフェローニ法では有意水準αを検定を行う数mで割ることで、FWERをα以下に抑えます。
なぜボンフェローニ法だとα以下におさまるのか
ボンフェローニ法では各検定の有意水準がα/mに設定されるわけですが、直感的にはなんとなく有意水準を分割することで総合してもα以下に抑えられることはわかると思います。
では、なぜそうなるのか、どういう点で厳しすぎるのかということを数式から考えてみたいと思います。
まずは証明から。
最初にFWERを数式で表します。検定を行う数をm、有意水準をα、各試験のp-valueを\(p_i(i=1,2,…,m)\)で表します。するとボンフェローニ法におけるFWERは
\(FWER=P(\bigcup_{i=1}^{m_0}(p_i\leq\frac{\alpha}{m}))\)
となります。これがα以下になるのを証明したいわけです。
ここで出てくる\(m_0\)は仮説検定を行うもののうち、帰無仮説が正しい数(実際は求められない)です。定義上αエラーが生じるのは帰無仮説が正しい場合なので、納得できるように思います。よって\(0\leq m_0\leq m\)であることが分かります。
続いてこのままでは計算が進まないのでブールの不等式を用いて不等号を立てます。
\(P(\bigcup_{i=1}^m(p_i\leq\frac{\alpha}{m}))\leq \sum_{i=1}^{m_0}P(p_i\leq\frac{\alpha}{m})\)
この不等式は至極普通の話で、各事象(例えばA1,A2,…とする)の和集合の確率はそれぞれの事象の起こる確率の和より小さくなるということです。\(m_0=2\)のときをベン図で考えるとこのような感じになります。
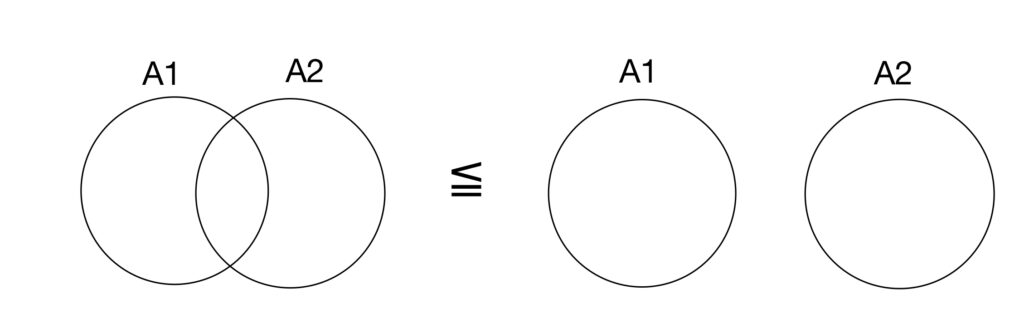
図のように共通部分がある場合は各事象の和集合の確率(左辺)の方が小さくなりますね。証明は後に載せておきます。
さてここで帰無仮説が正しいときなので
\(P(p_i\leq\frac{\alpha}{m})=\frac{\alpha}{m}\)
となります。これを用いて先程の式を見ていくと
\(P(\bigcup_{i=1}^m(p_i\leq\frac{\alpha}{m}))\leq \sum_{i=1}^{m_0}P(p_i\leq\frac{\alpha}{m})\\=m_0\frac{\alpha}{m}\\\leq m\frac{\alpha}{m}\\=\alpha\)
となるので、ボンフェローニ法を用いた補正ではFWERが必ずα以下になることが証明できました。
ボンフェローニ法はどう厳しいのか
さて、ここで式の等号が成立する条件を考えてみます。一つ目の不等号は各事象が互いに素なときに成立します。いわゆる確率の公理と呼ばれるもので、σ-加法性の仮定によるものです。
実際的には臨床試験で複数のアウトカムを検定する場合、各事象が互いに素であるというのは少し考えにくい場面のようにも思います。最近ボンフェローニ法を見たものだとパーキンソン病薬のオピカポンの試験で使われていました。
実際の医学論文から統計を学んでみるⅥ -多重検定/ボンフェローニ法/ファミリーワイズエラー率- – 脳内ライブラリアン
3種類の用量のオピカポンとプラセボの比較で3回検定を行うのでここにボンフェローニ法が使われているわけですが、それぞれの検定は互いに素ではない可能性の方が高いように思われますね。一つの用量で効果があれば同様に他の用量でも効果がある確率は高いように思われるので、ある程度厳しい条件になっているのではないかと思ってしまいます。
続いて二つ目の不等号は\(m_0=m\)となるときに成立します。つまり、検定をする仮説が全て実は帰無仮説が正しい場合です。これは実際には知りようがないのでなんとも言えませんが、検証的な試験であれば検定しようとしている内容は通常対立仮説が正しいことを念頭に置いているように思うので、さすがに全て帰無仮説が正しいということは多くないのではないでしょうか。この辺はどの程度効果が期待される内容かにもよると思うのですが、この意味でも厳しい基準と言えそうですね。
ただ基準が厳しくなるとはいえ、比較的大きいサンプルサイズだと有意水準を満たす効果サイズ(effect size)は通常の有意水準とさほど大きく変わらないということも指摘されているようです。
この差が実際的に意味のあるほどの差でないので、わざわざそこまで厳しい基準にする意味はなく、p-valueを提示しつつ指標の一つとして考えてもらうぐらいで良いのではないかという意見のようです。厳しい基準を用いると偽陰性がどうしても増えてしまうので、十分な理由なく一つの基準で有効無効の2値を判断するのはあまり好ましくないですね。
おまけ:ブールの不等式の証明
可測空間\((\Omega, \mathcal{F})\)上の確率測度Pにおいて\(A_1, A_2,…,A_n\in\mathcal{F}\)とする。
ここで\(A_1=B_1, A_k\setminus\bigcup_{i=1}^{k-1}=B_k(k\geq2)\)とすると、\(B_k\)は互いに素になるので確率の公理を用いて
\(P(\bigcup_{k=1}^nA_k)=P(\bigcup_{k=1}^nB_k)\\=\sum_{k=1}^nB_k\leq\sum_{k=1}^nA_k\)
となります。なお、無限の場合でも同様となります。
参考文献
Bonferroni correction – Wikipedia
最近ハマってます。測度論を避け続けてきた結果、難しく感じますがきちんと確率の基礎となる概念を学べるように思います。
















コメントを残す