引き続き6章から。
問3はどうにも腑に落ちないところがあったので
問4に続きます。
θの条件付き確率、一様分布、順序統計量、不偏推定量
そして平均2乗誤差の問題ですね。
まず(1)から p.119の例題と同様にして解きます。

一様分布の場合は定義関数で表します。
定義関数をみるとθと関連しているのがX(n)であるのがわかります。
あらかじめ知っていないとわからないですね、これ。
続いて(2)
平均2乗誤差(mean square error : MSE)のどちらがより小さいかを求める問題。
『MSE=分散 – biasの2乗』 でしたが
不偏推定量であればMSEのbiasは0になるので
要は分散を求めて比較すればよいわけです。
不偏推定量の定義からE[θhat]=θとなるので
それを利用して求めます。
θhatが十分統計量X(n)の関数として表されるので
X(n)の確率密度関数を使います。

一様分布の標本平均なのでE[Xbar]のほうはさらっと求めます。
まずX(n)の不偏推定量から

続いて標本平均は

引き算すると明らかにU2>U1であることがわかります。
では最後、最尤推定量のMSEを求めます。
(1)で求めた同時確率密度関数から、θを最小とすれば
最も確率が大きくなることがわかります。
θ=X(n)のとき最小なので

となります。

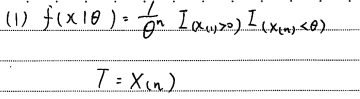

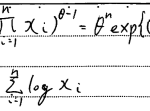













コメントを残す