問1に続いて、問2についてみていきたいと思います。
2変量の確率関数に関する問題です。ちょっと初っ端からあまりみない出題のされ方で面食らってしまい、全然できませんでしたが、基本に立ち返って落ち着いて解けばなんとかできそうな問題でした。変数変換も必要となる問題ですが、一昨年の統計検定数理と同様に変数変換した後の値域には常に注意が必要ですね。
一応以下のような解き方が解答を導き出せましたが、結構泥臭くてもっとスマートに解けそうな気もするので、もし良い解答ご存知の方がいたらご教示ください。
*2023.1.13追記:コメントでもっと簡単な解法について教えていただきました。追加で記載します。有難うございました。
なお問1の解答例はこちら
(1)
まずは周辺累積分布関数を求める問題。問題文には同時累積分布関数しかないので、そこから順番に変形して求めていきます。
まずは同時確率密度関数を求めましょう。
F(u,v)をuとvで微分すれば良いので
\(f(u,v)=\frac{1}{4}\)
となります。
続いては周辺確率密度関数を求めて
\(f(u)=\int_{-1}^{1}\frac{1}{4}dv=\frac{1}{2}\)
続いて周辺累積分布関数を求めれば
\(F(u)=\int_{-1}^u\frac{1}{2}dt=\frac{u+1}{2}\)
となります。F(v)の場合も全く同様なので
\(F(v)=\frac{v+1}{2}\)
となります。
(2)
(1)の結果から
f(u,v)=f(u)f(v)
となることがわかりますので、UとVは独立だとわかります。
またそれぞれは区間[-1,1]の一様分布に従います。
(3)
まず\(P(U^2+V^2\leq1)\)を求める問題。
さてこの式を見ていると極座標に変換したくてうずうずなってこないでしょうか。そんな訳で変換してみます。
\(u=rcos\theta, v=rsin\theta\)
なおこの時ヤコビアンはrとなり、確率密度関数は
\(f(r,\theta)=\frac{r}{4}\)
となります。
また、(3)の条件式のもとでは値域が\(0\leq r\leq1, 0\leq\theta\leq2\pi\)となります。
よってその値域全体で積分すれば良いと言えます。
\(\int_0^1f(r,\theta)dr=\frac{1}{8}\)
続いてθで積分して
\(\int_0^2\pi\frac{1}{8}d\theta=\frac{\pi}{4}\)
となるので、解が求まります。
(4)
続いては\(U^2-2UV+V^2\leq1\)の確率の問題。
この式は
\((U-V)^2\leq1\\-1\leq U-V\leq1\)
と変形できます。
ここで再び変数変換を使っていきます。u=s, u-v=tとおくとヤコビアン(の絶対値)は1になるので
\(f(s,t)=\frac{1}{4}\)
となります。
ここで、値域は
\(-1\leq s\leq1\\-1\leq s-t\leq1\)
となり、sの値域はtの正負によって場合わけされることがわかります。
まず
①\(t\geq0\)のとき
\(-1+t\leq s\leq1\)
このとき、tを周辺化すると
\(f(t)=\int_{-1+t}^1\frac{1}{4}ds\\=\frac{1}{2}-\frac{t}{4}\)
となります。
また
②\(t\lt0\)のとき
\(-1\leq s\leq1 t\)
となります。
同様にして
\(f(t)=\frac{1}{2}+\frac{t}{4}\)
です。
さて、求めたい式に戻って
\(P((U-V)^2\leq1)\\=P(-1\leq T\leq1)\\=P(-1\leq T\lt0)+P(0\leq T\leq1)\\=\int_{-1}^0(\frac{1}{2}+\frac{t}{4})dt+\int_0^1(\frac{1}{2}-\frac{t}{4})dt\\=\frac{3}{4}\)
となります。
(5)
(5)では(4)の結果を利用しながらVの期待値を求めていきます。これまた泥臭く解いていくしかできなかったのですが、スマートなやり方を知りたいです。
先ほどと同様の変数変換を用いるとV=S-Tとなりますので\(U^2-2UV-V^2\leq1\)の条件つき確率分布でS-Tの期待値を求めていきます。
\(E[S-T|-1\leq T\leq1]\\=\int\int(s-t)\frac{1}{4}\frac{4}{3}dtds\\=\int_{-1}^0\int_{-1}^{1+t}\frac{(s-t)}{3}dtds+\int_0^1\int_{-1+t}^1\frac{(s-t)}{3}dtds\\=0\)
続いてVの分散を求めるため\(V^2\)の期待値は
\(E[(S-T)^2|-1\leq T\leq1]\\=\int_{-1}^0\int_{-1}^{1+t}\frac{(s-t)^2}{3}dtds+\int_0^1\int_{-1+t}^1\frac{(s-t)^2}{3}dtds\\=\frac{5}{18}\)
かなり計算過程を割愛してます。
Vの分散については期待値が0であることから\(V^2\)の期待値と一致するため上記が答えとなります。
最後に相関係数ですが
Cov(U,V)=E[UV]-E[U]E[V]
となるものの、E[V]=0となることにより結局はE[UV]を求めれば良いことがわかります。
E[UV]もゴリ押しすると
\(E[UV]=E[s(s-t)]\\=\int_{-1}^0\int_{-1}^{1+t}\frac{s(s-t)}{3}dtds+\int_0^1\int_{-1+t}^1\frac{s(s-t)}{3}dtds\\=\frac{5}{36}\)
相関係数ρは
\(\rho=\frac{\frac{5}{36}}{\frac{5}{18}}\\=\frac{1}{2}\)
というわけでゴリゴリ計算して解けましたが、果たして本番にこのような時間があるかというと間違いなくないのが問題ですね。
(3)のスマートな解答
さて、コメント欄で教えていただいた解答ですが、u,vが一様分布にあることを利用してグラフにおける面積で考えて解く方法です。
まずu,vの通常の同時分布は以下に示すグラフ(2×2の正方形)の面積で表されます。いつもの雑な手書き図で歪んでいてすみません。
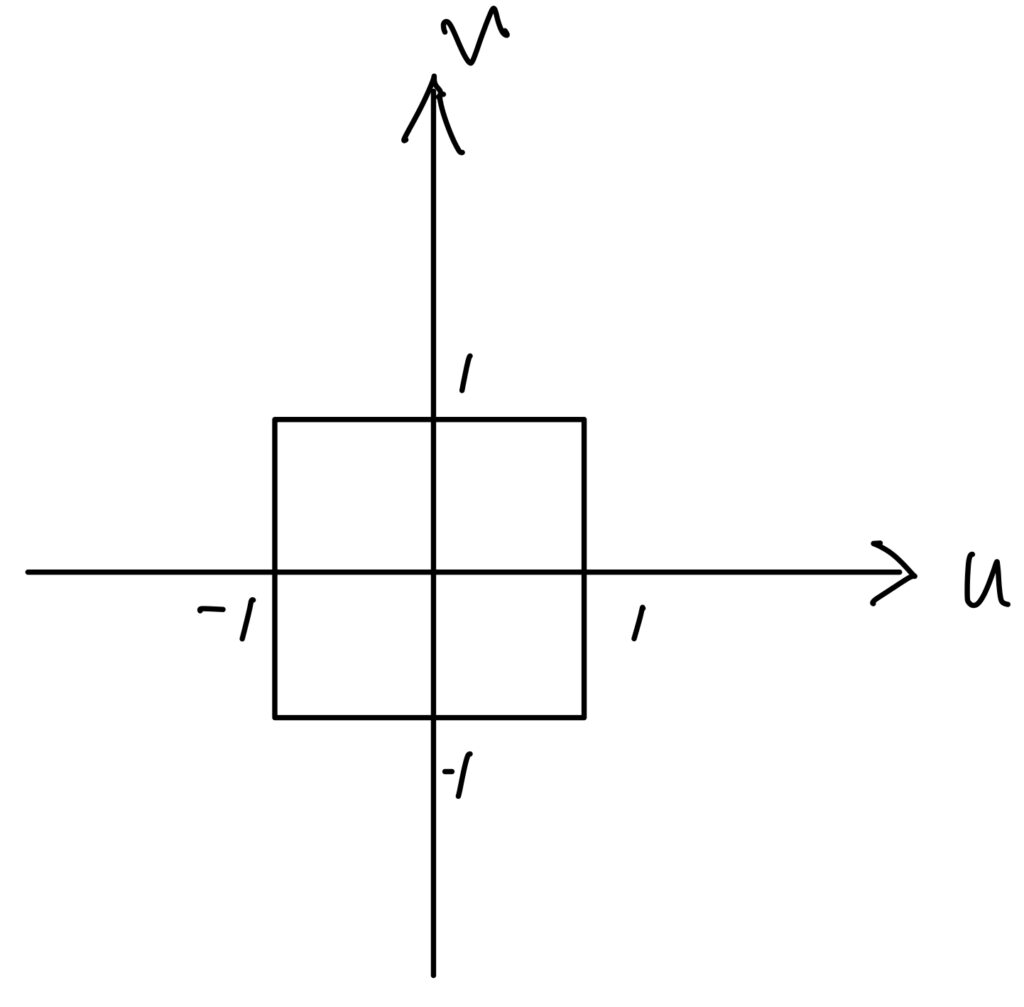
ここで、今回求める確率である
\(P(U^2+V^2\leq1)\)は以下のような図の面積で表されます。
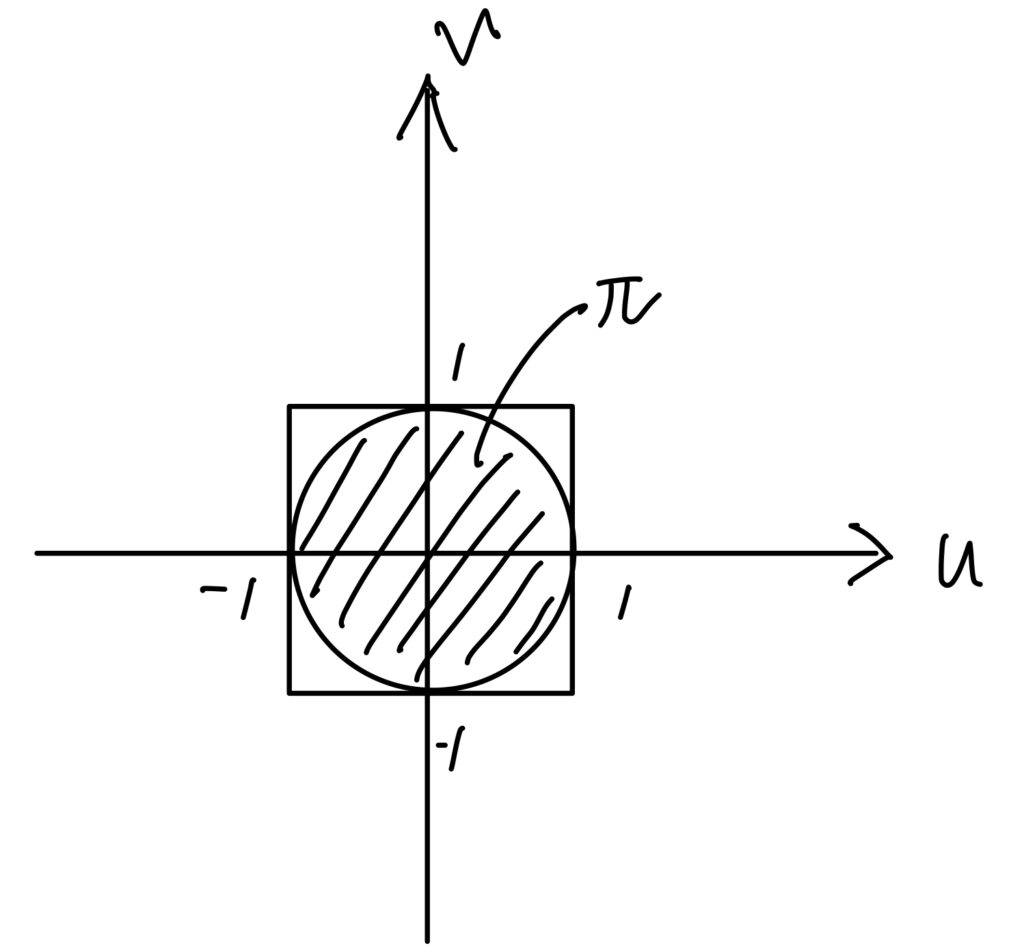
確率について考えるとこの面積4の正方形が1を表すため、面積πの部分を確率に直すと
\(\frac{\pi}{4}\)となります。ス、スマートすぎる。己の愚直さを嘆きたくなりますね。
(4)のスマートな解答
こちらも上記と同様の手順でサクッと解けるようです。
求めたい確率の式を変形すると
\(P(-1\leq U-V\leq1)\)
となるので、これを図に表すと
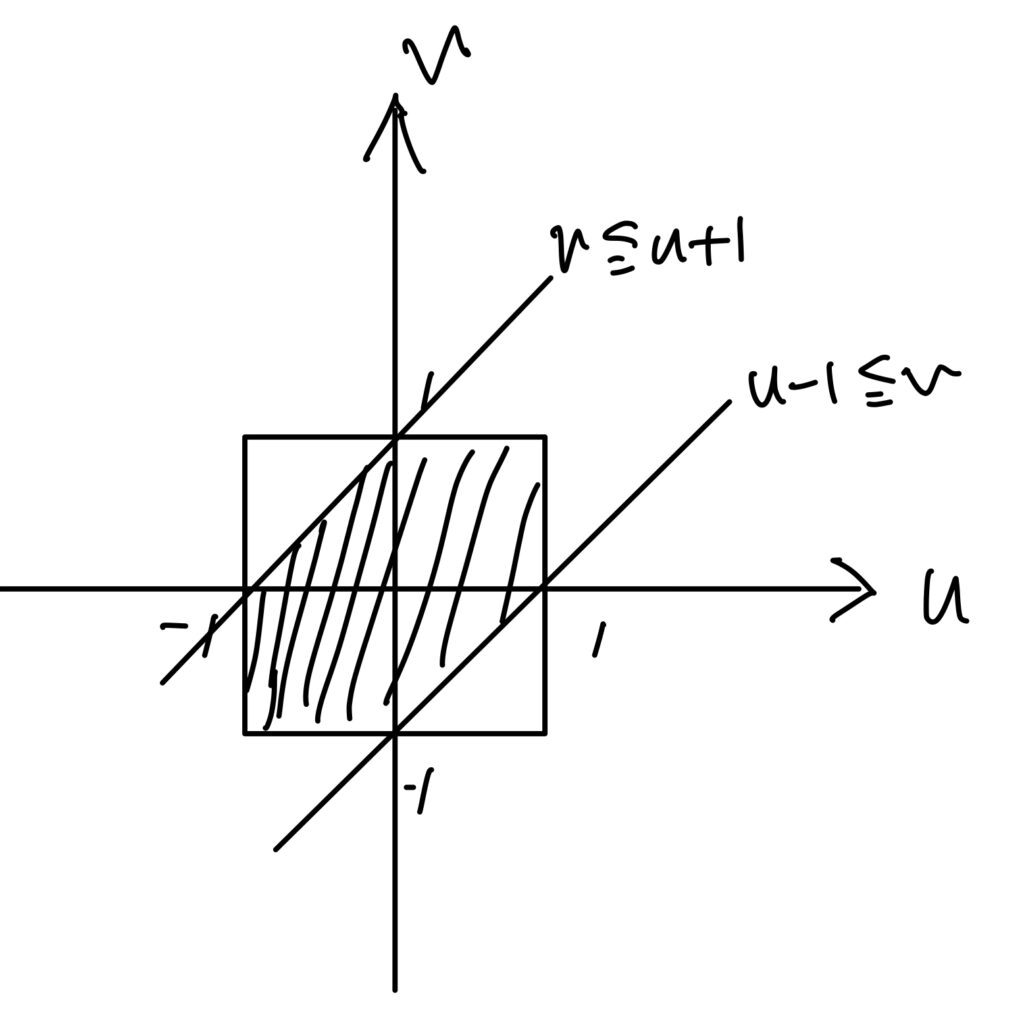
となります。斜線部分の面積は3となりますので、(3)と同様に考えて
\(\frac{3}{4}\)
となります。
統計学をどんどん自分で学んで深めたい、という方へのおすすめ書籍をこちらのページの下部にまとめております。初心者向けのものから応用まで幅広く読んでいますので参考にどうぞ。

















いつも解説記事ありがとうございます。
昨年、統計数理を受験した者です。
この問題は、同時確率分布が一様分布であることを利用して、
(3)、(4)は変数変換せずに、規程範囲の面積を掛けるだけで瞬殺する方法があるようです。
例えば(3)はf(u,v)×π(半径1の面積)、(4)はf(u,v)×3 (2×2 正方形の3/4の面積)
この考え方の延長で、(5)も面積で考えると、変数変換不要の様です。
コメントありがとうございます。いつもtwitterも楽しく拝見させていただいております。
解き方のご教示ありがとうございました!納得いたしました。
やっぱりこんな泥臭い方法ではなかったんですね笑
また時間が取れましたら記事の方にも追記させていただきます。