現代数理統計学の基礎 6章 問15
久々になりましたが統計学基礎の解説に戻ります。 問14は3章の別の問題の結果を多用しすぎていて 正直解説が若干めんどくさい、、、ので問15。 母数θを用いた関数の不偏推定量について 与えられるクラメールラオの不等式の問題...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説久々になりましたが統計学基礎の解説に戻ります。 問14は3章の別の問題の結果を多用しすぎていて 正直解説が若干めんどくさい、、、ので問15。 母数θを用いた関数の不偏推定量について 与えられるクラメールラオの不等式の問題...
 統計
統計実際の論文をみつつ統計学習をしてきましたが 今回の論文についてはここでいったん最後です。 使用している論文がこちら “Neck weakness is a potent prognostic factor...
 医学
医学引き続き 実際の論文をみつつ統計の学習してみます。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sporadic amyotr...
 医学
医学さて、ログランク検定が具体的に何をしているのか 掘り下げてみようと思います。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sp...
 統計
統計前回から続きまして 実際の論文をみつつ統計の学習してみます。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sporadic a...
 統計
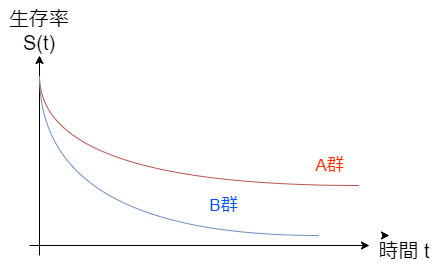
統計今回は医師向けの内容です。 最近数理統計学をそれなりに勉強したので 多変量解析とか生存時間解析などの 応用分野に手を伸ばし始めています。 これでようやく普段読む論文の解析内容に近づいてきました。 そこで、論文...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説(4) は \( n \to \infty \) のときの漸近分布を求める問題。 これも解答に誤植があるのかなという気がしますが。 (3) で使ったように \[ \frac{x_i^2}{\theta} \sim \ch...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続いて(3)ですが。 \[ \frac{n\hat{\theta}}{\theta} \] がどのような分布に従うかという問題。 順番に考えます。 まず問題の条件から \[ \hat{\theta} = \frac{...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説(2)の問題。 (1)で求めたθの最尤推定量を求めて 平均と分散を求めていく問題。 最尤推定量はさほど難しくはなくて 対数尤度関数=0をおいて導出します。 まず同時確率密度関数から。 \(f_n(x|\theta)=\f...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説平均0, 分散θの正規分布についての問題。 まず(1)は分散のフィッシャー情報量を求める問題ですね。 問12で書いたように対数尤度関数の二回微分を求めていけばよいので、まず対数尤度関数が \[ \log f(x|\the...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説続いて(3) 最尤推定量の分散がクラメールラオの下限に一致することを 確かめる問題です。 まず最尤推定量を確かめるため 同時確率密度関数の最尤推定をします。 同時確率密度関数を \( f(x_n|\lambda) \) ...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続いて(2)ではポアソン分布のクラメール・ラオの下限を調べます。 予備知識として クラメール・ラオの下限は n個のデータのフィッシャー情報量を \( I_n(\theta) \) として \[ \frac{1}{I_...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、数理統計学の勉強ですが 問題を解くことはすでにこの本の8章まで 終わってまして、回帰分析の勉強をぼちぼち開始しました。 復習がてら引き続き6章の解答を。 問12はポアソン分布の最尤推定の問題です。 (1)は積率母関...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説コロナ流行のため電車通勤→車通勤に変えたのですが そのせいで普段の通勤中にできていた勉強ができず 統計の勉強も滞り気味で困っているところです。 間空きましたが統計の問題続けていきます。 6章問11の(2)です。 最尤推定...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説二項分布における不偏推定量と最尤推定量の問題ですね。 Bin(n,p)のpの推定は簡単ですが 今回の問題はθ=p(1-p)について。 p2乗が出る分若干計算が要ります。 まず対数尤度は \[ \log L(p) = \l...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続き問10から(3) σとμの不偏推定量を求める問題。 不偏推定量とは \[E[\hat{\theta} (X)] = \theta\] を満たす推定量のことでした。 (2)より \( \frac{2T}{\sigm...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説気を取り直して引き続き6章の問10(2)。 これがなかなか面倒くさい問題ですね。 まずは同時確率密度関数で式を表します。 p.104より順序統計量の同時確率密度関数は n! × それぞれの確率密度関数の積なので \[ f...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説頑張ってLatex使って書いてみよう、という気持ちで問10。 指数分布の問題。 まず(1)、μとσの2つの母数に関しての十分統計量の問題。 定義関数を用いつつ、同時確率密度関数を出します。 あとからU=X(1)をくくりだ...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説今まで手書きの汚い数式を晒してきたのですが 今後色々まとめなおしたりする時に 何だかんだでPCで数式を書けるようにする必要があることを と思い直しまして。 結局スキャナでメモを読み取るのも面倒くさいのと 計算手書きで...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説最近コロナコロナと言いすぎたので また引き続き統計学の続きを。 次もベイズ法による事前分布・事後分布の問題。 まずは(1) 本文p124の最下段に記載ありますが 事後分布による推測は十分統計量がわかればよいの...
最近のコメント