関数の期待値の不等式を考えるときに役立つイェンセンの不等式と、それが成立するために必要な凸関数の定義についてざっくりみていきます。
凸関数とは
凸関数とは下側に凸な構造を持つ関数のことです。
\(y=x^2\)
などが典型的でわかりやすいかと思います。
定義はいくつかありますが、よく用いられるのは以下の式です。
\(f(\gamma x+(1-\gamma)y)\leq\gamma f(x)+(1-\gamma)f(y)\)
となるとき、\(0\lt\gamma\lt1\)、区間\(x,y\in I\)上において
f(x)は凸関数であるといえます。
これは式を変形すると以下のような状況と同値となります。区間x,yの間にあるzに対してのf(z)は、x,yの間に引いた直線に対して常に下側に存在します。
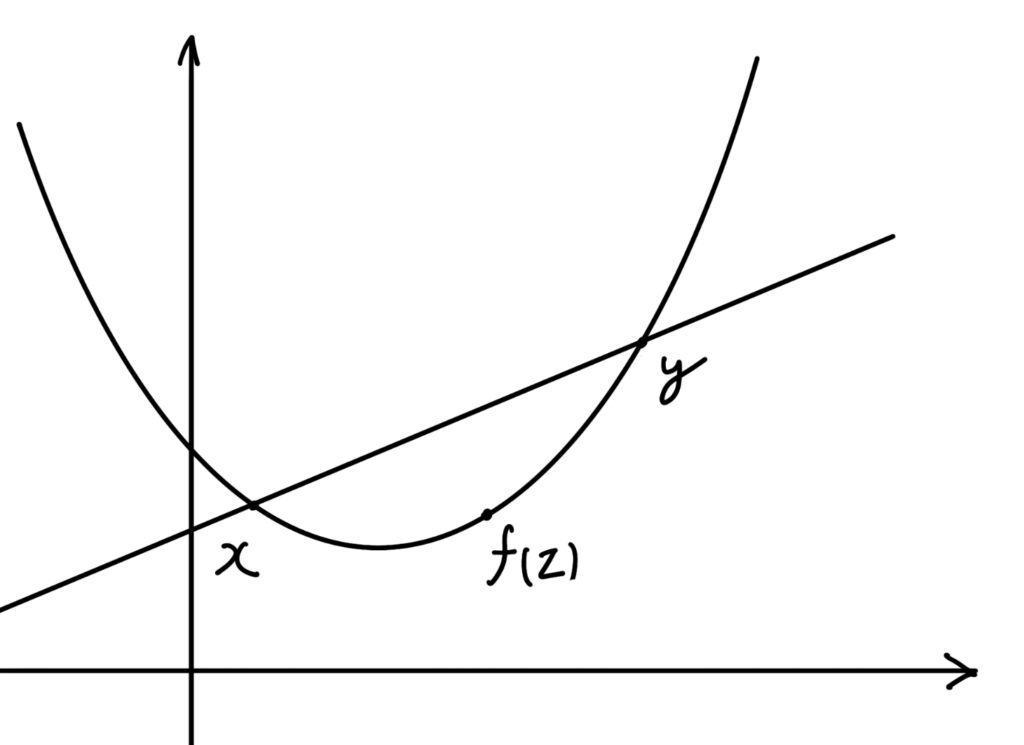
また便利な点として2次導関数(f’’(x))≧0とも同値となっています。
証明はこちらを参考にすると簡潔でわかりやすいです。
この凸関数であることを条件にして用いることができるのがイェンセンの不等式です。
Jensenの不等式
統計に関連して期待値について述べる場合、イェンセンの不等式は以下のような式となります。
f(x)を凸関数とすると
\(f(E[X])\leq E(f(x))\)
なぜこの様になるのか直感的にわかりやすい証明を考えてみます。
f(x)が凸関数の時、その接線は必ずf(x)より下側を通ることを利用します。
期待値の点におけるf(x)の接線は傾きをbとして以下の式で表すことができます。
\(f(E[X])+b(x-E[X])\leq f(x)\)
図で表すとこんな感じです。
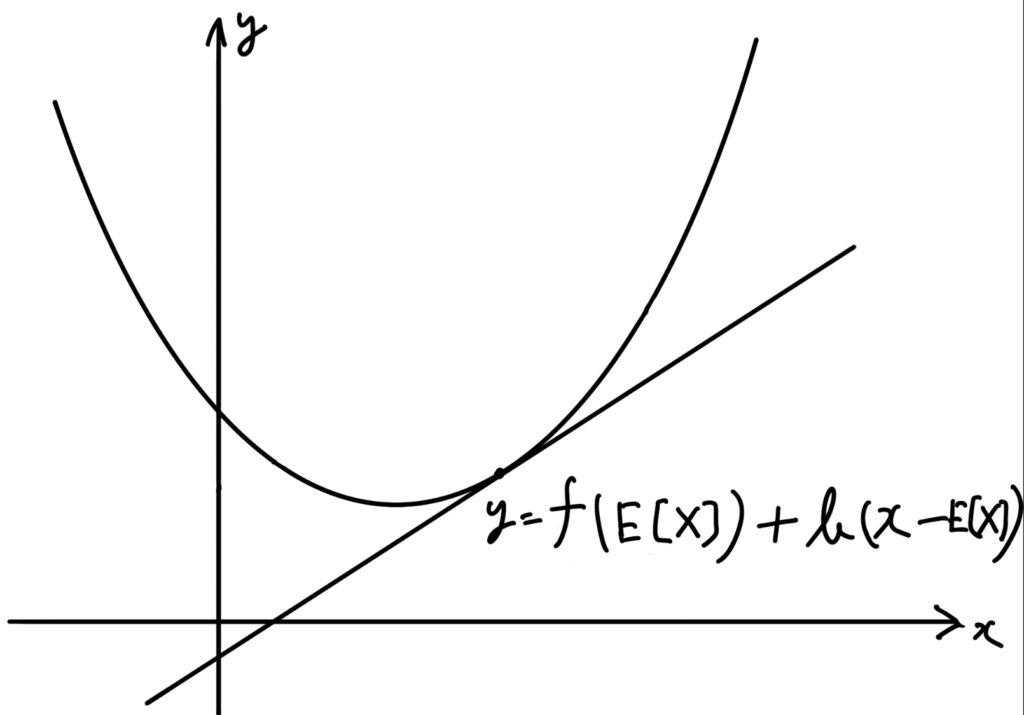
あとは両辺について期待値をとります。
\(E[f(E[X])]+E[b(x-E[X])\leq E[f(x)]\)
さて左辺の第1項は定数であり、第2項は0となるので
\(f(E[X])\leq E(f(x))\)
となります。イェンセンの不等式を使った具体的な問題例は現代数理統計学の基礎の第2章の問題にありましたので、こちらもご参照ください。















コメントを残す