現代数理統計学の基礎　5章　問8

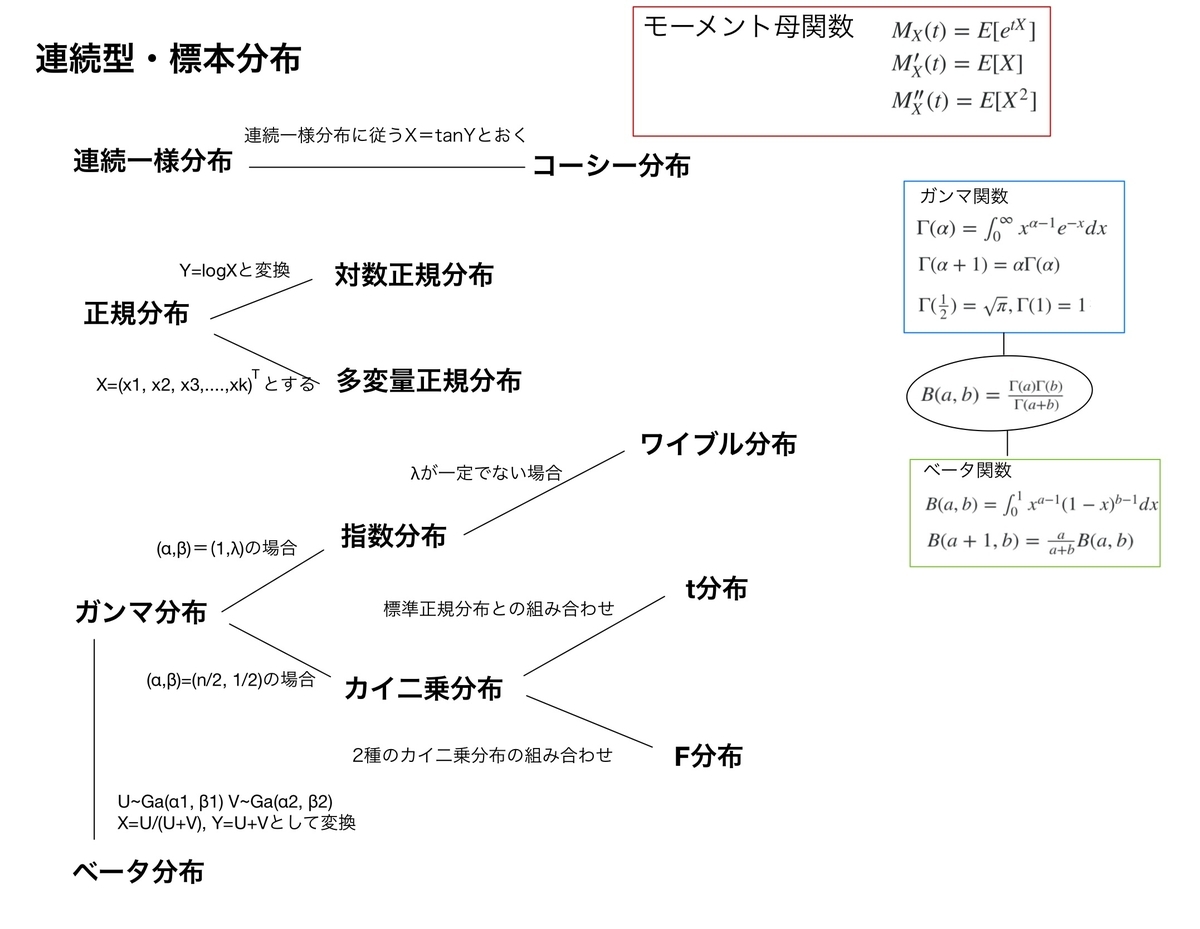
ちまちまと「現代数理統計学の基礎」の忘れてる分野の解き直しを行ってます。色々忘れてますけど、やり直すたびに少しずつ理解が進むのは嬉しいことですね。

5章の問8は平均二乗収束を示す問題ですね。

確率収束を示す問題ではチェビシェフの不等式もしくは平均二乗収束を使うことが多いので、統計検定1級でも同様の解き方は結構役立つのではないでしょうか。

分散が分かりやすい、かつ不偏推定量の収束を示すなら、チェビシェフで良いと思うのですが、今回の問題のように複雑な形で不偏推定量ではない場合は平均二乗収束の方が良いんですかね。

式を見ていきますと

\(E\left[\left(\frac{2}{n(n+1)}\sum jX_j-\mu\right)^2\right]\\=\frac{4}{n^2(n+1)^2}E\left[\left\{\sum jX_j-\frac{n(n+1)}{2}\mu\right\}^2\right]\\=\frac{4}{n^2(n+1)^2}E\left[\sum j(X_j-\mu)\right\}^2\right]\)

さてここで、期待値の中はどうなっているかを和の記号をバラして具体的に見てみると

\(\{(X_1-\mu)+2(X_2-\mu)+…+n(X_n-\mu)\}\times\{(X_1-\mu)+2(X_2-\mu)+…+n(X_n-\mu)\}\)

ですね。

そうなると

\((X_1-\mu)\times2(X_2-\mu)\)

みたいなのは期待値を取ると0になって消えることがわかります。これはシグマと期待値が出てくるときには結構よくある変形の手段ですね。

なので同じデータ部分を二乗したもののみが残ります。よって

\(=\frac{4}{n^2(n+1)^2}E\left[\sum j^2(X_j-\mu)^2\right]\\=\frac{4}{n^2(n+1)^2}\frac{1}{6}n(n+1)(2n+1)\sigma^2\\=\frac{2n+1}{3n(n+1)}\sigma^2\)

n→∞のとき、0に収束することがわかります。よって、μに確率収束することが示せました。