現代数理統計学の基礎 5章 問5
統計応用もやりつつ、時々統計数理のほうも解いていっています。 今回は5章の問5。 順序統計量と平方変換の両方を使う良い問題です。 まずZ=min(X, Y)なのですが、これをどう表現するか。 解答例と同様に、順序統計量と...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説統計応用もやりつつ、時々統計数理のほうも解いていっています。 今回は5章の問5。 順序統計量と平方変換の両方を使う良い問題です。 まずZ=min(X, Y)なのですが、これをどう表現するか。 解答例と同様に、順序統計量と...
 日常生活/家電/ガジェット
日常生活/家電/ガジェット統計の話題が続きすぎたので、たまには全然違う日常の話を。 4月から妻が再度働き始めることもあって、現在自宅では家事時短に向けた取り組みが粛々と進められています。 そんなわけで最近電気圧力鍋を購入しました。 「豚の角煮」を...
 日常生活/家電/ガジェット
日常生活/家電/ガジェットblogの記事にするほどではないけれど、「本の感想を書きたい」「論文の紹介をしたい」「医療関連のニュースをさらっと紹介したい」「統計検定1級の勉強の辛さを共有したい!」ということがたまにあります。 そういった内容を書...
 倫理・医療社会
倫理・医療社会さて、最近認知症関連の話題で注目されているのはbiogenとエーザイが開発しているモノクローナル抗体、アデュカヌマブ(aducanumab)です。 アルツハイマー型認知症の治療薬として期待されており、アミロイドβを標...
 統計
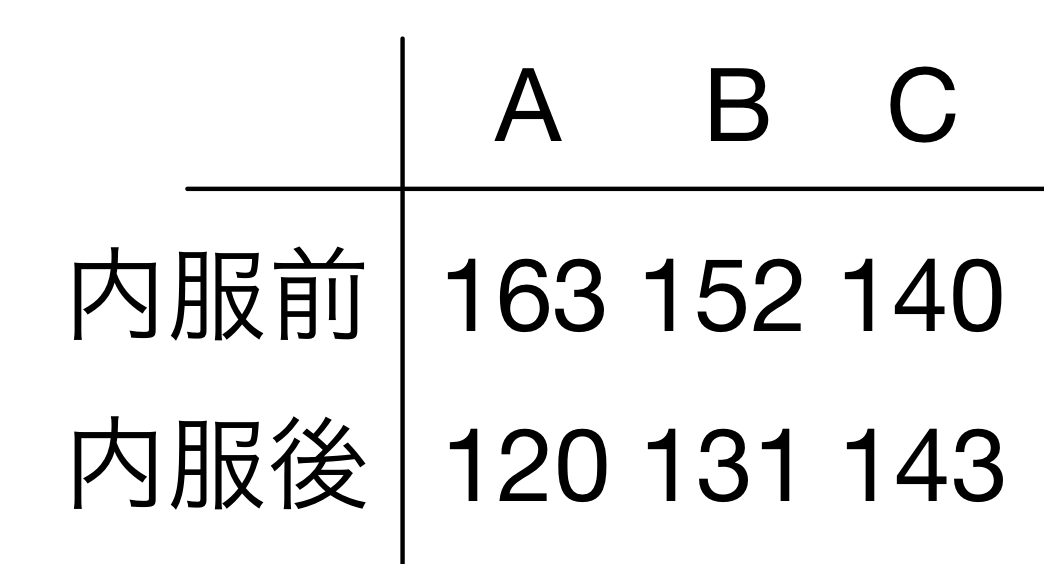
統計引き続きノンパラメトリック法の検定についてみていきます。 ウィルコクソンの符号付き順位検定とは ウィルコクソンの符号付き順位検定は1標本の検定に使われるもので、対応するデータの差が正のときに1、負のときは0として(こ...
 統計
統計2016年、2019年と出題されているノンパラメトリック法の検定について簡単にまとめておきます。 符号検定とは 符号検定は1標本に対して行われるノンパラメトリック検定です。ある対応するデータの差が正であれば1、負であれば...
 医学
医学引き続き生存時間解析の話ですが、2019年の過去問ではRMST法の問題が出ていたので、期待値と分散の導出について簡単に説明します。 RMST法ってそもそもなんやねんということは過去に一度記事を書きました。 mediboo...
 医学
医学生存時間解析の勉強を進めて、今回はCox比例ハザードモデルについて過去問に対応できるように知識をつけていきたいと思います。 ハザード関数と生存関数の知識が前提に必要なので、わからなかったらこちらをどうぞ。 mediboo...
 医学
医学今回はカプラン・マイヤー推定値の信頼区間を知るための分散の求め方をやってみようと思います。この分散の式はGreenwoodの公式と呼ばれています。 統計検定1級の教本にも紹介されていますし、導出の過程はほどほどの難しさな...
 医学
医学今日も統計検定1級の統計応用・医薬生物学分野について頻出の内容をまとめてみようと思います。 追加した内容は以前まとめた記事に載せていきます。 統計検定1級の出題範囲と過去の記事・お役立ちサイト・参考書をまとめてみた【統計...
 医学
医学統計数理もだいぶ勉強は進んできたのでぼちぼち統計応用の分野の勉強も進めようかと思っています。 そこで2018−2019年の過去問をようやく買ってみて統計応用・医薬生物学分野をみてみたのですが、思った以上に難しそうでした、...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説淡々とまた解いていきます。 問11は互いに独立でない場合けれど、今日分散が0に収束するときの、標本平均の確率収束を考える問題です。 他の問題でも用いられますが、確率収束を示す場合、収束する値との差を十分小さい値εを用いる...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説二項分布を変数変換したときの、確率収束及び分布収束の問題ですね。 今まで解答の意味がよくわからなかったのですが、確率変数 \(X_n\) が \(n \to \infty\) となるときにどう動くかは、前提として二項分布...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説続いて分布収束の問題です。 不偏分散と母分散を用いた式が分布収束することを示す問題ですね。 \[ \frac{n}{n-1} \frac{1}{n} \left\{ \sum (x_i – \mu)^2 \r...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、戻りまして5章の問題をぼちぼち解いていきます。 統計応用の方も対策を進めたいので、並行してやっていきたいところですね。 問10は確率収束、分布収束の問題です。 まずは(1)から。 (1)はn→∞のとき、不偏分散が母...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、(3)は一様最強力不偏検定を示す問題です。 公式の解答を見ると \(\sqrt{n}|x| > z_{\frac{\alpha}{2}}\) が一様最強力不偏検定である から唐突に始まってます。 それを導出し...
 統計
統計今回は初見では意味が分かりづらかった不偏検定、一様最強力不偏検定とその証明について、正規分布の場合を例に記事にまとめておこうと思います。 不偏検定とは? 不偏検定(unbiased test)とはざっくり言うと、仮説検定...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説7章問10は一様最強力検定が存在しないことを示す問題です。 複合仮説でも片側検定であれば、成り立ち得ますが、両側検定だと成り立たないことは本書中でも、棄却域を示す式が異なることで説明されていました。同様の方法で示します。...
 日常生活/家電/ガジェット
日常生活/家電/ガジェットさて、11月に初代iPad airからiPad air 4への大幅な変更を果たしたのですが、使い勝手が最高すぎるので、改めて使用感を書いてみます。 medibook.hatenablog.com 新しい機器が出るたび...
 『現代数理統計学の基礎』解説
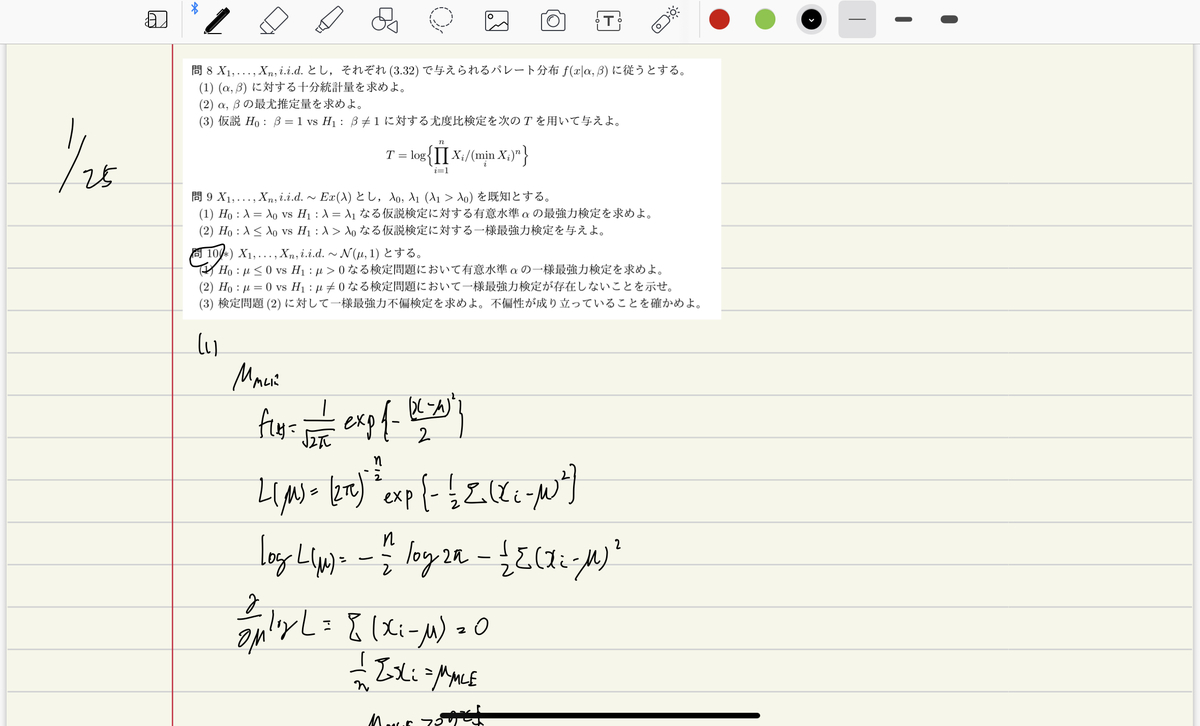
『現代数理統計学の基礎』解説このところ淡々と問題をやり続けてます。次は問10。 今回は正規分布を使った複合仮説の仮設検定ですね。 まず今までの7章の問題と同様に帰無仮説を\(\mu=0\)として尤度比検定(=最強力検定)を求めます。 まず正規分布に...
最近のコメント