実際の論文から統計を学んでみる④-ログランク検定は何をしているのか-超幾何分布
引き続き 実際の論文をみつつ統計の学習してみます。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sporadic amyotr...
 医学
医学引き続き 実際の論文をみつつ統計の学習してみます。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sporadic amyotr...
 哲学・倫理・医療社会
哲学・倫理・医療社会前回に続いて読書術の本紹介をします。 「知識を操る超速読術」Daigo 「読んだら忘れない読書術」 樺沢紫苑 「読書の技法」 佐藤 優 前回記事はこちら 読書術について書かれた本をまとめてみる① – 脳内...
 哲学・倫理・医療社会
哲学・倫理・医療社会読書術についての本は以前から ちょくちょく読んでいたのですが 自分の読書経験もそこそこに増えてきたので なんとなく自分が正しいなと感じる読書術と そうでない読書術がわかれてきました。 そこで、今まで読んだ読書術本をま...
 医学
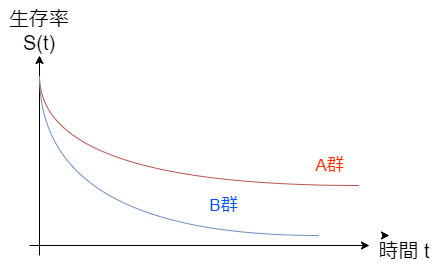
医学さて、ログランク検定が具体的に何をしているのか 掘り下げてみようと思います。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sp...
 統計
統計前回から続きまして 実際の論文をみつつ統計の学習してみます。 使用している論文がこちら “Neck weakness is a potent prognostic factor in sporadic a...
 統計
統計今回は医師向けの内容です。 最近数理統計学をそれなりに勉強したので 多変量解析とか生存時間解析などの 応用分野に手を伸ばし始めています。 これでようやく普段読む論文の解析内容に近づいてきました。 そこで、論文...
 哲学・倫理・医療社会
哲学・倫理・医療社会職場において 「もっとこれをこうしたら仕事が楽になるなあ」と改善したいことや 問題が生じて「どうしたら同じことが起きないようになるだろう」と 思った際に、提案が常に必要とされます。 また、医師としてどのようなキャリア...
 哲学・倫理・医療社会
哲学・倫理・医療社会読みたい本は結構溜まってきているのですが コロナ感染を少しでも防ぐために車通勤にしているもので オーディオブックしかできないんですね。 家と職場では読む時間もかなり限られるので。 なので、愛用のオーディオブック.jp...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説(4) は \( n \to \infty \) のときの漸近分布を求める問題。 これも解答に誤植があるのかなという気がしますが。 (3) で使ったように \[ \frac{x_i^2}{\theta} \sim \ch...
 哲学・倫理・医療社会
哲学・倫理・医療社会以前紹介した瞑想実践アプリ「headspace」ですが Basicsコースの10回分が終わったので実感含めた感想を書いてみます。 前回記事はこちら 瞑想アプ&#...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続いて(3)ですが。 \[ \frac{n\hat{\theta}}{\theta} \] がどのような分布に従うかという問題。 順番に考えます。 まず問題の条件から \[ \hat{\theta} = \frac{...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説(2)の問題。 (1)で求めたθの最尤推定量を求めて 平均と分散を求めていく問題。 最尤推定量はさほど難しくはなくて 対数尤度関数=0をおいて導出します。 まず同時確率密度関数から。 \(f_n(x|\theta)=\f...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説平均0, 分散θの正規分布についての問題。 まず(1)は分散のフィッシャー情報量を求める問題ですね。 問12で書いたように対数尤度関数の二回微分を求めていけばよいので、まず対数尤度関数が \[ \log f(x|\the...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説続いて(3) 最尤推定量の分散がクラメールラオの下限に一致することを 確かめる問題です。 まず最尤推定量を確かめるため 同時確率密度関数の最尤推定をします。 同時確率密度関数を \( f(x_n|\lambda) \) ...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続いて(2)ではポアソン分布のクラメール・ラオの下限を調べます。 予備知識として クラメール・ラオの下限は n個のデータのフィッシャー情報量を \( I_n(\theta) \) として \[ \frac{1}{I_...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、数理統計学の勉強ですが 問題を解くことはすでにこの本の8章まで 終わってまして、回帰分析の勉強をぼちぼち開始しました。 復習がてら引き続き6章の解答を。 問12はポアソン分布の最尤推定の問題です。 (1)は積率母関...
 哲学・倫理・医療社会
哲学・倫理・医療社会コロナの話が多い中、何かと自粛で外出できない日々ですが 以前から気になっていたマインドフルネスを教えてもらえるアプリ 「headspace」を試してみました。 いろんな本に書いてある割には意外と記事がなかったので書いてみ...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説コロナ流行のため電車通勤→車通勤に変えたのですが そのせいで普段の通勤中にできていた勉強ができず 統計の勉強も滞り気味で困っているところです。 間空きましたが統計の問題続けていきます。 6章問11の(2)です。 最尤推定...
 哲学・倫理・医療社会
哲学・倫理・医療社会データ解析について色々ネットで調べていたときに たまたま紹介されていた本ですが面白かったので紹介します。 題名は 『ソーシャル物理学 「良いアイデアはいかに広がるか」の新しい科学』 文庫 ソーシャル物理学: 「良...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説二項分布における不偏推定量と最尤推定量の問題ですね。 Bin(n,p)のpの推定は簡単ですが 今回の問題はθ=p(1-p)について。 p2乗が出る分若干計算が要ります。 まず対数尤度は \[ \log L(p) = \l...
最近のコメント