現代数理統計学の基礎 5章 問10(2)
続いて分布収束の問題です。 不偏分散と母分散を用いた式が分布収束することを示す問題ですね。 \[ \frac{n}{n-1} \frac{1}{n} \left\{ \sum (x_i – \mu)^2 \r...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説続いて分布収束の問題です。 不偏分散と母分散を用いた式が分布収束することを示す問題ですね。 \[ \frac{n}{n-1} \frac{1}{n} \left\{ \sum (x_i – \mu)^2 \r...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、戻りまして5章の問題をぼちぼち解いていきます。 統計応用の方も対策を進めたいので、並行してやっていきたいところですね。 問10は確率収束、分布収束の問題です。 まずは(1)から。 (1)はn→∞のとき、不偏分散が母...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説さて、(3)は一様最強力不偏検定を示す問題です。 公式の解答を見ると \(\sqrt{n}|x| > z_{\frac{\alpha}{2}}\) が一様最強力不偏検定である から唐突に始まってます。 それを導出し...
 統計
統計今回は初見では意味が分かりづらかった不偏検定、一様最強力不偏検定とその証明について、正規分布の場合を例に記事にまとめておこうと思います。 不偏検定とは? 不偏検定(unbiased test)とはざっくり言うと、仮説検定...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説7章問10は一様最強力検定が存在しないことを示す問題です。 複合仮説でも片側検定であれば、成り立ち得ますが、両側検定だと成り立たないことは本書中でも、棄却域を示す式が異なることで説明されていました。同様の方法で示します。...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説このところ淡々と問題をやり続けてます。次は問10。 今回は正規分布を使った複合仮説の仮設検定ですね。 まず今までの7章の問題と同様に帰無仮説を\(\mu=0\)として尤度比検定(=最強力検定)を求めます。 まず正規分布に...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説問9(2)ですが、問4と同じような感じで棄却域を広げていきます。 現代数理統計学の基礎 7章 問4 – 脳内ライブラリアン まずは帰無仮説を \( \lambda = \lambda_0 \) と固定します。...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説現代数理統計学の基礎、7章の問9です。 指数分布において、最強力検定=尤度比検定を求める問題ですね。「指数分布=ガンマ分布の特殊形」であることが問題を解くのに役立ちます。 まず尤度関数は \( L(\lambda) = ...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説(3)は尤度比検定を求める問題ですね。 まず尤度比を求めます。公式の解答は一発の式変形で何が何やらわかりませんが、もう少し詳しく見てみます。 \( \frac{L(\hat{\alpha}, \beta_0)}{L(\h...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説問8の(2)をやります。最尤推定量の問題です。 まず、 \( \alpha \) の最尤推定量 \( \hat{\alpha} \) は尤度関数と条件から決まります。 (1)で見たように、条件から \( \alpha \...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説最近論文やら発表やらが溜まり気味であんまり更新する余裕がありません、、。そして、今年は人事異動で仕事も増える+神経内科専門医試験もあるので、統計検定1級に受かる自信がじわじわ削がれるわけですが。 ひとまず、あんまり細かく...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説引き続いて、問7(3)です。 (2)で出てきたZがどんな分布になるかという問題。 公式の解答では当然のごとく、ガンマ分布に従う確率変数 \(X, Y\) であれば \[ \frac{X}{X+Y} \sim B(n,m)...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説代表的な確率分布の特性についてまとめおわったところで、問7です。 確率分布の特徴と関連するので、記事を参考にしながらご覧ください。 medibook.hatenablog.com まずは(1) 指数分布の確率関数の和の分...
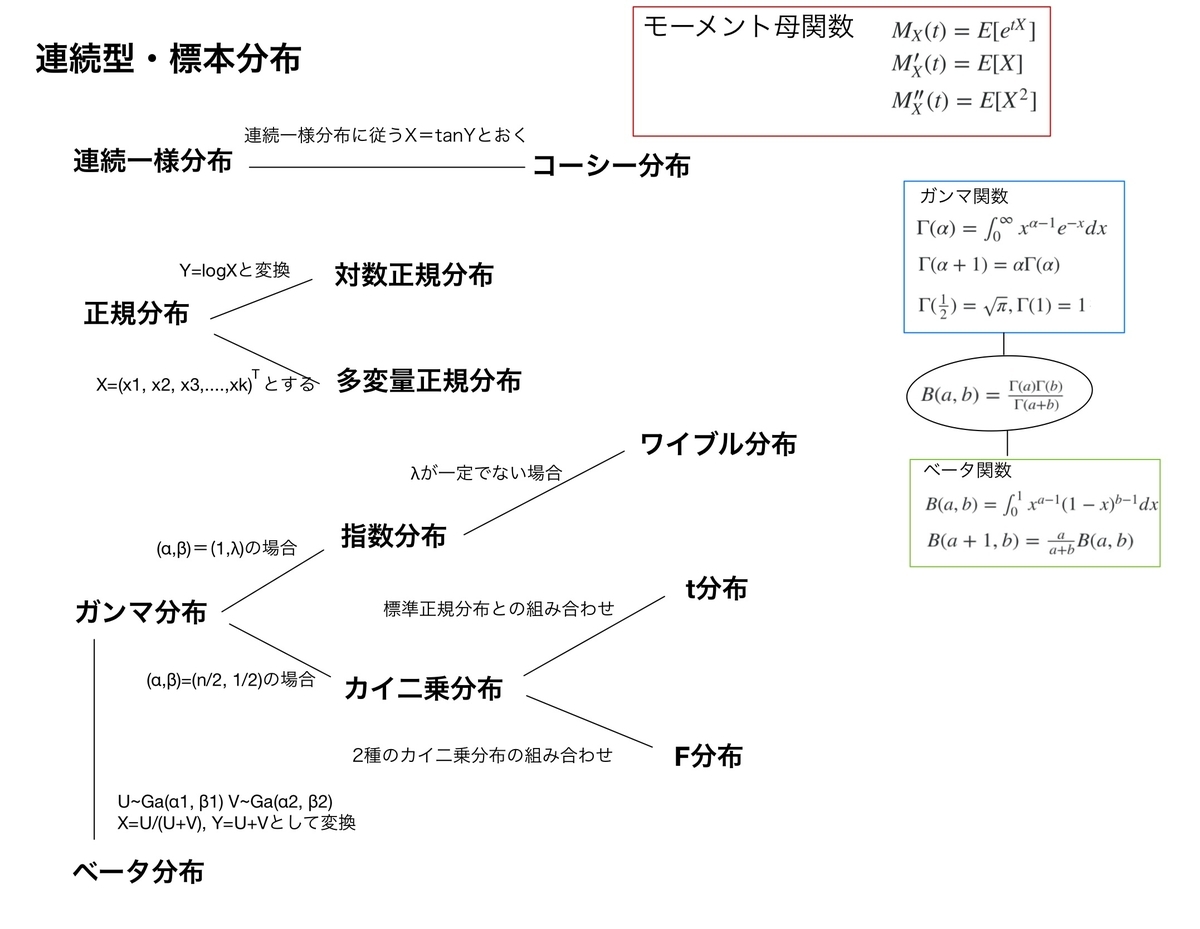 統計
統計前回に引き続いて統計検定1級に出てきやすい連続型確率分布・標本分布について、関係性と式を簡単にまとめてみます。 前回の記事はこちら medibook.hatenablog.com 図にしてみる 各分布の式など モーメント...
 統計
統計別記事で代表的な確率分布についてまとめていますが、文量が増えそうなのでワイブル分布の平均と分散の計算はここでまとめてみます。 そういえばワイブル分布については今までほとんど問題も解いたことなかったですし、馴染みがあまりあ...
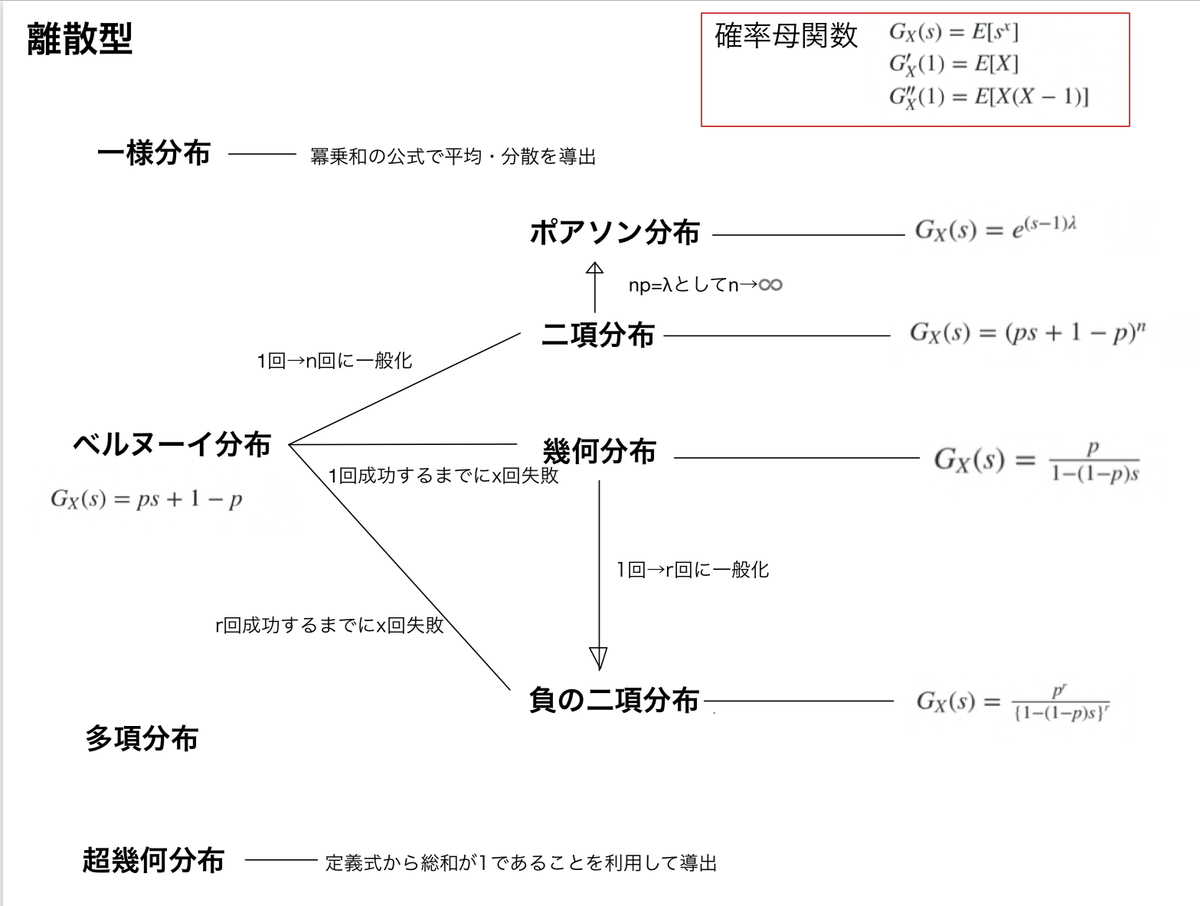 統計
統計明けましておめでとうございます。 さて、今年も統計の勉強記事からあげていきます。 統計検定1級において確率分布は基本事項として問題を解く際に前提知識として必要なことも多いですが、その特徴自体が問題として問われることもあり...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説7章問6は分散の異なる二つの正規分布における尤度比検定とその棄却域の問題です。 1問目は分散の比をλとして、単純仮説の尤度比検定を求めていきます。 まず帰無仮説下において、 \[ \sigma^2_Y = \lambda...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説今回の問題はポアソン分布における尤度比検定・ワルド検定・スコア検定の問題ですね。これも基本に沿ってやれば問題なくできます。 同じ内容を扱った過去記事はこちら medibook.hatenablog.com ま...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説今回は問4、指数分布の問題ですね。 この問題は指数分布モデルにおいて臨床試験で必要とされる症例数計算なんかの話と結びついており、ネット上に同じ話を論じている南山大学のPDFがあったので、参考になるかもしれません。 htt...
 『現代数理統計学の基礎』解説
『現代数理統計学の基礎』解説問3は結構込み入った内容となってますので説明入れながらやっていきます。 目次: (1) (2) <捕捉>フィッシャー情報行列について ワルド検定 スコア検定 (3) (1) まずは(1)から。 今...
最近のコメント